by soo jin lee
9.Examine graphs of
of different values of a, b, and c.
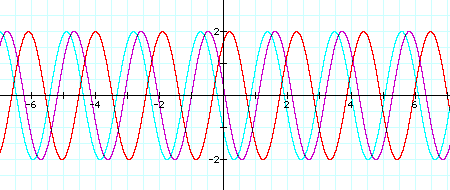
1.Fix a=2, b=3, then see what happens to c.
when c=1, c=3 and c=10,

From above, we can see clearly that the graph constantly changes to the left as the value of c increases.
considering what I have done above, I came out with two important messages.
1. Maximum and Minimum value is not influenced by the value of 'c', and the value of 'a' determines the Maximim and Minimum value of the graph.(If a=2, Max. =2 & Min.=-2)
2.Although the value of 'c' changes, there is no difference at cycle
2. Fix a=2, c=1, then see what happens to 'b'
when b=1, b=3 and b=10
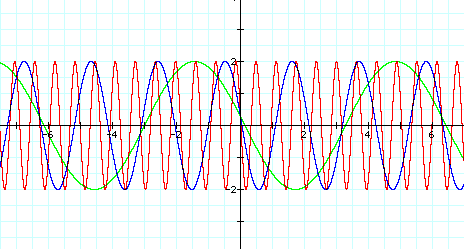
from above I can see a little difference from 1,
although the maximum and minimum value don't change, the value of 'b' alter the cycle of the graph!
3.Fix b=1, c=2, then see what happens to 'a'
when a=1, a=3, a=10
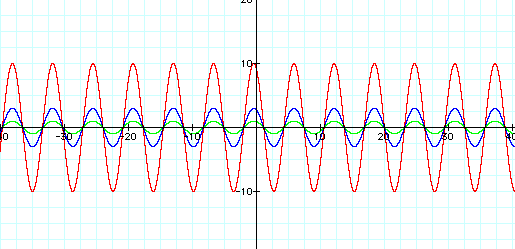
Isn't it very interesting graph??^^
unlike 1 and 2 above,
The value of 'a' affects the maximum and minimum value!
However this time the cycle is not affected.
As a result, we can see the value of 'a' influences the maximum and minimum value of the graph,
the value of 'b' effects the cycle of the graph, and finally the value of 'c' has no impact on any of Max. and Min. or the cycle of the graph!