by Soo Jin Lee
Investigate
Note:
* When a and b are equal, and k is an integer,
this is one textbook version of the " n-leaf rose."
* Compare with
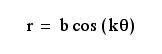
for various k. What if . . . cos( ) is replaced with sin( )?
1.Let's explore the graph
when the value of a=b=k=1, the graph below is shown.
Now let's see the characteristics of each of the a, b, k.
To look over the charecteristic of "a", I will first fix the two value "b", "k" as 1 and substitute various values into "a"
from above, we can see the value of "a" determines the point on y-axis.
i.e a=1, the graph passes +1,-1 of the y-axis
a=2, the graph passes +2,-2 of the y-axis.
In addition, it seems like the distance between the center and the x-intercept is the value of "a".
However the assuption I have built changes when the value of "a" is negative.
To see the distinction of the graph when "a" is positive and negative, click here.
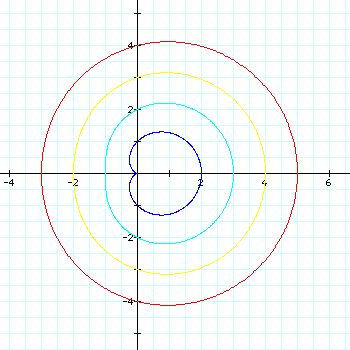
To look into the character of "b", fix a=k=1 and substitute various points into "b".
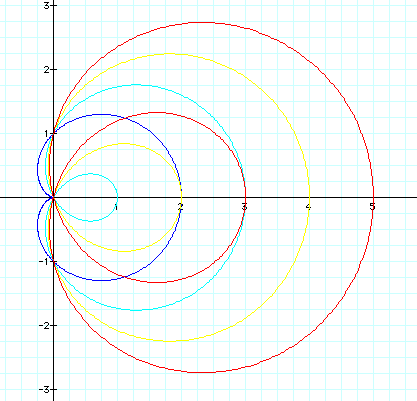
First they all passes the origin. Except for the first graph that the value of b=1, other three graphs have similar shapes and characteristics; they all have small circle inside of their large circle. In addition, the value If "b" influences the graph's x-intercept; for example, when b=1, it passes through 0 and 2, when b=2, it passes through 1 and 3. It seems like the graph passes the b-1, b+1 points on the x- axis.
to see further investigation( changes the value of "b" from negative to positive), click here
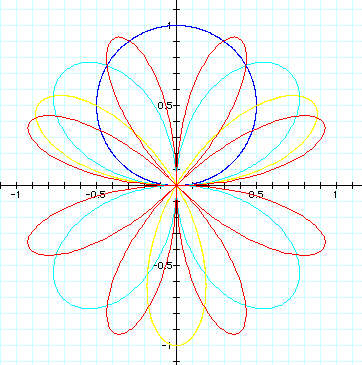
To explore the character of "k", I will fix the a=b=1 and changes the value of "k".
This investigation will show you "n-leaf rose."
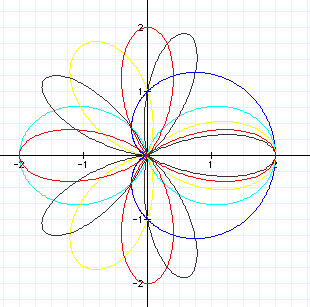
From the above graph, we can learn the "n-leaf rose".
"k" value influences the number of leaf of the graph; for example, the graph has 2 leaves when k=2 and the graph has 3 leaves when k=3 and so on.
Since cos(-
)=cos
, the number of leaf will be same altough
the value of "k" has the negative value.
Further investigation shows more fascinating graphs; to see the animation, click here.
2. compare the graph with
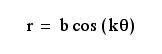
when I fix b=1, I can also see the "n-leaf roses".
As we can see from the picture, the graphs are similar to the graph we've investigated first.
However we can find out a difference which
resulted from the value of "a"; the distance form the
center to the end of the leaf are depended by the value of "a".
when the value of "a" was 1, the distance form the center
to the edge of leaf was 2, when the value of "a" was
0, the distance from the center to the edge of leaf is 1. Further
exploration will show you that the distance from the center to
the edge of the leaf is "
+1".
click here to see.
If we fix the value of k as 1 and substitute the various numbers to "b",
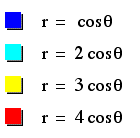
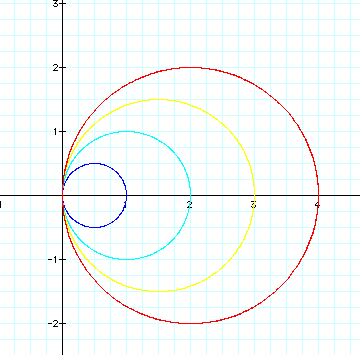
to compare with the graph 
,
when there was "a", we had a strange shape circle, but
we now have real circles. We can see more in here.
3. what if cos is replaced by sin??
Investigate the graph
.fixing the value of of a=b=1. we will see the influence of k.
compare two pictures below.
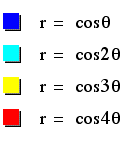
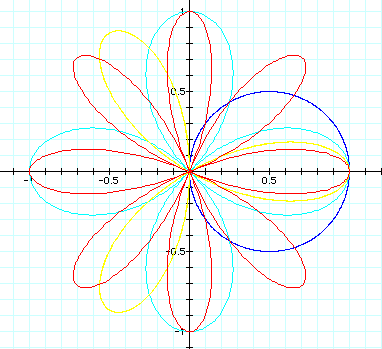
from the above pictures, we can see the graph rotated to the left 90 degree from the cosine graph.
considering cos(x)=sin(y/2 -x), it is trivial to see that conclusion.