Consider the locus of the vertices of the set of parabolas graphed from
Show that the locus is the parabola
Generalize.
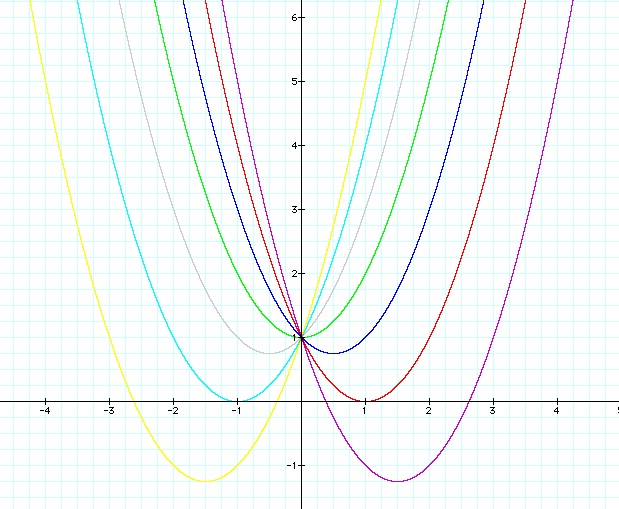
See the graph when b=-3, -2, -1, 0, 1, 2, 3
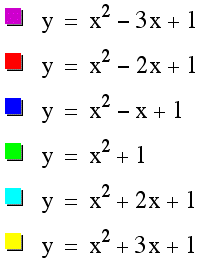
![]()
generalization of this graph,
1) The common value of these six graphs are '1'
2) When b < -2, there are two intersects at x-axis which means that we have two positive roots.
3) When b = -2, there is an intercept at x-axis which means that we have one positive roots.
4) When -2 < b < 2, no points intersect with x-axis which means that we have as imaginary root.
5) When b = 2, similar to when b=-2, there is an intercept at x-axis however we have it now at the negative side of the x-axis. we have one negative root.
6) When b > 2, similar to when b<-2, there are two intersects at x-axis however at the negative side of the x-axis. we have two negative roots.
Let's find the locus of these graphs! If you want to see the movement of the locus, click the "exploration" botton below.
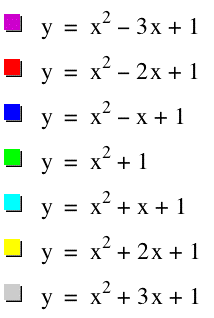
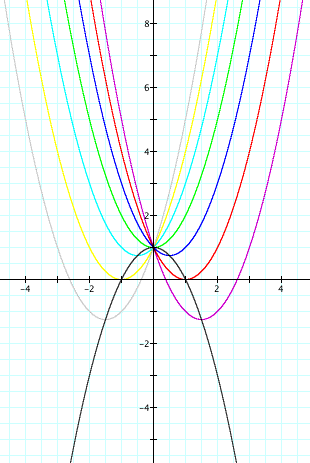
As you can see from the above picture, the locus of the equation Y = X^2 + bX + 1 is Y = -X^2 + 1.
Let's further our investigation!!
Consider again the equation X^2 + BX + C = 0,
since I cannot use B at the graphic calculator, I will use the term Y instead.
let's forst consider the case when C = 1, 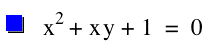
then you will get the graph like below.
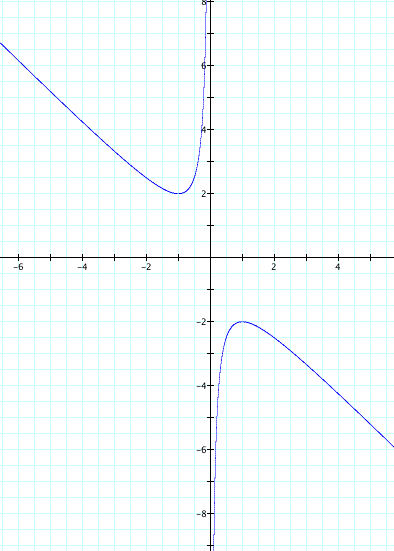
Take arbitrary points to the Y value, and overlap to to the above graph.
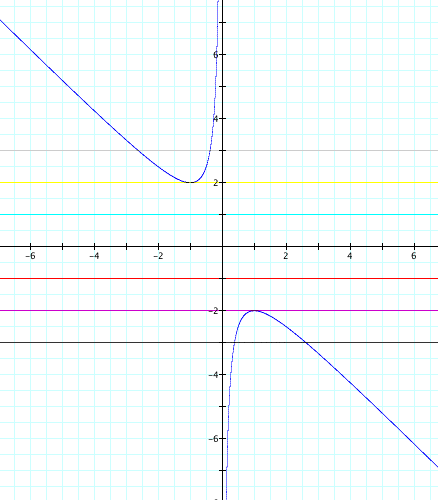
From the above graph, we can clearly see these results;
when y > 2, there are two negative real roots,
when y = 2 and y = -2, there are one real roots for each value of y.
when -2< y < 2, there are two imaginary roots.
when y<-2, there are two positive real roots.
What if the graph is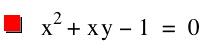 ?
?
I will do the same process as I did before,
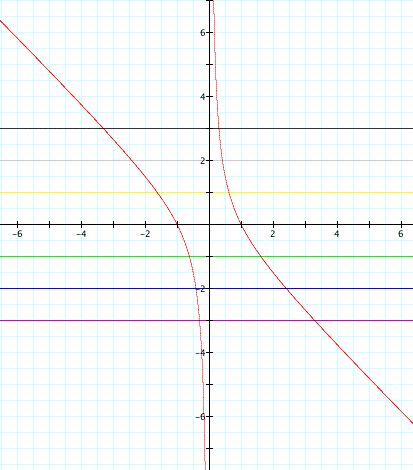
Now the result is totally different from the one we did before,
Whatever the value of y is, there are always one negative root and one positive root.
We can generalize our investigation like below.
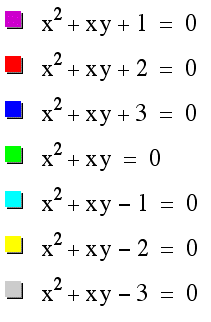
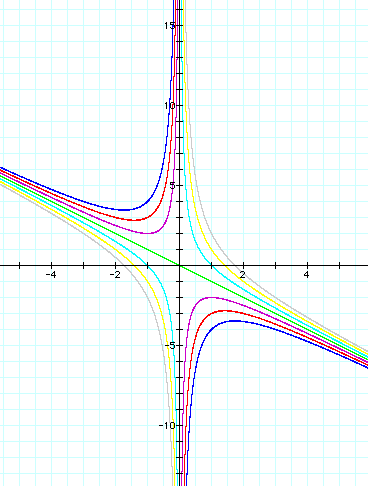
When C > 0, roots of the equation depended on the value of y
however when C < 0, there will always be one positive and one negative root for the equation.