by Soo Jin Lee
3. Use your script tools to construct the tangent circle to two given circles if the given point is on the smaller of the two circles
* a. so that the smaller circle is internal
to the tangent circle.
* b. so that the smaller circle is external to the tangent circle.
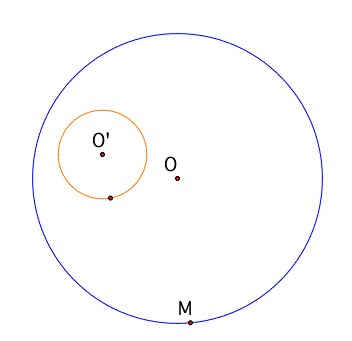
a. First draw one large circle and put one smaller circle inside the large one.
Be sure to put arbitrary points for each circle.
From now on, for the convenience, I will indicate larger circle as circle A and smaller circle as circle B. I let circle A's origin as O and circle B's origin as O'.

now we need to construct a line which passes through O and the point I have arbitrary dotted at the circle A. And make a circle C which has the same radius as circle O' and the origin is at M.
then indicate the intersection between the line and the circle C as N.
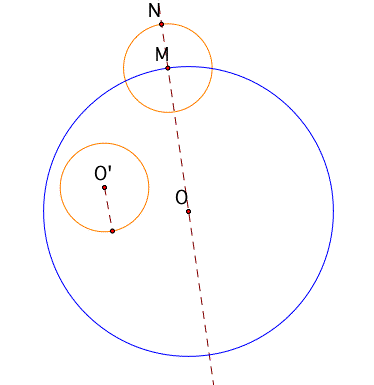
Draw a segment between N and O', and make a midpoint at that segment NO'.
By building a perpendicular line from that midpoint, I can get the intersection P between that line and the line which passes through the circle A.
finally make a circle where the origin is at the point P,
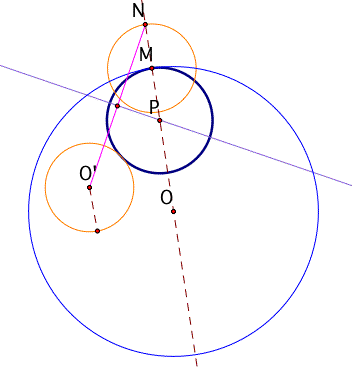
Now, as you can see, the dark blue circle from the above picture is "TANGENT CIRCLE".
let's further our investigation to see the locus of the center of the tangent circle.
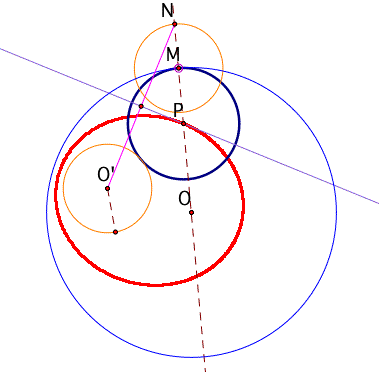
I get the ellipse shape for the locus of the center of the tangent circle.
to see the animation, click here.
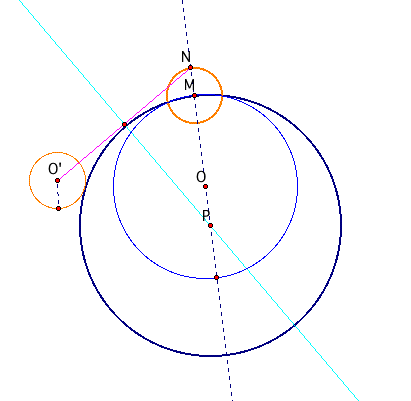
b. smaller circle external to the tangent circle.
I made a same process as above, first I draw a large circle O and a smaller circle O', then I put each of the circle arbitrary points.
I made a line which passes through orgin at the circle O and the arbitrary point I made at that circle.
Next I put the point M, N(like the picture below) which are the intersection of the line and the large circle.
Thrn I made a segment through N and O', put the midpoint then make a perpendicular line from that point.
I get the intersection P by drawing the perpendicular line and I will use the point as the origin of tangent circle.
Now the dark blue circle below is the "TANGENT CIRCLE"!!!!!
What kind of locus will I get from the above tangent circle?
I further my exploration to see this.
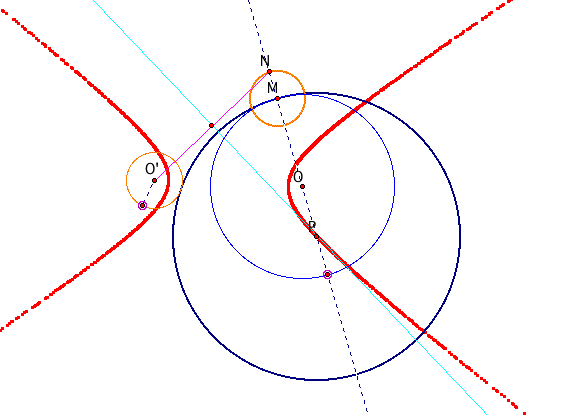
I found interesting thing by finding out the locus of the point P.
Considering that the only different thing I have done from the above case was the putting the smaller circle outside of the larger circle,
I expected to get a similar locus as when the smaller circle is inside of the tangent circle, but I got totally different shape.
I got something like parabola!!!!
To see the animation, click here