

By Soo Jin Lee and Jaehong Shin
A4 size is the most frequent used paper size in various kinds of documents including copying paper. The standard size of A4 paper is 297mm * 210mm. As we can see, that numerical value is not simple. Why did people decide such a complex size? For example, if it were designed in the size of 300mm * 200mm, that seems to be much simpler and more convenient. When we calculate the ratio of 297 to 210, we can get about 1.414. It is also different from the Golden Ratio ( 1.618), one of the most famous ratios in the world. Where did the numerical value come from?
It is known that Deutsche Industrie Normen suggested such a size in order to minimize the loss of paper in the process of smaller size paper by cutting the larger one. That is, the first largest original paper should has a good shape itself and the smaller one after being divided in halves also should keep up their good shape. It is desirable to get the smaller one without cutting out some part of the paper in the middle of repeating such process.
From now on, I will investigate several different paper sizes that have different ratios including current A4 size ratio: 3 to 2, 4 to 3, 1.618 to 1(Golden ratio) and 1.414 to 1 by using spreadsheet and GSP. Through exploring each size, we may be able to be aware of the most effective ratio that minimizes the loss of papers.
Since the size of the A0, the whole sheet of paper is 1189mm * 841mm, let start from the similar size that has maintain each ratio.
Say, X0: 1200 * 800 (3 to 2), Y0: 1200 * 900(4:3), Z0: 1200 * 742(Golden Ratio) and A0.
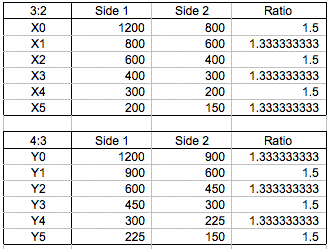
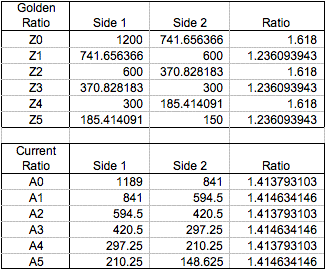
We can see that only A-series paper keeps thire ratio while being divided. Now, using GSP let's investigate what each paper looks like.
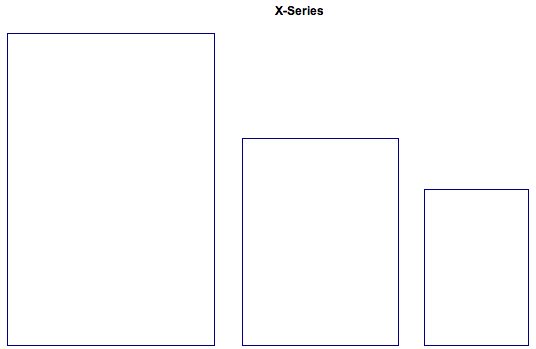
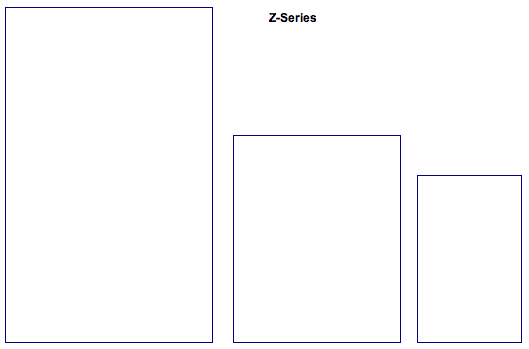
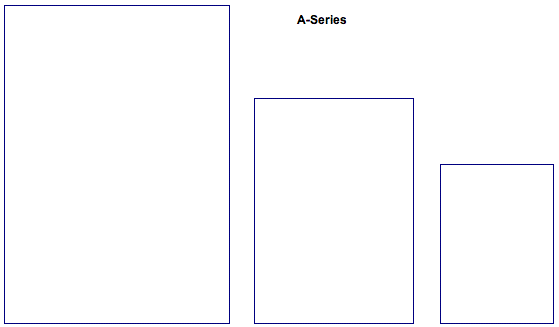
As we can see, only current A series keep up their ratios, that is, only A series maintain their similar figure. It means there is no need to cut out unnecessary parts while dividing paper in halves. For instance, when we divide X0 paper in halve. We can get two pieces of size 800mm*600mm and the ratio is 1.333. This rectangle looks stubby compared with the original one. To use this paper in real life, we have to cut off a part so that it has proper appearance. Y-Series and Z-Series also face same problem in order to be used in real life.
Through our investigation, it seems to be reasonable to set up the paper size as A-series since A-Series can be divided into smaller pieces with any loss of paper.
Then, how could it be found in the past? Let's analyze the beauty of paper mathematically. Maybe someone already noticed the fact, which 1.414 is approximate value of square root of 2.

Suppose that the ratio of the whole sheet of
paper is x:1, then the ratio of the half of the whole paper is
1:x/2 as we can see above.
To order that divided pieces is the similar figure to the original
one, x should satisfy the next propositional expression: x:1 =
1:x/2. From that expression, the quadratic equation x2 = 2 can
be induced and we get the solution, square root of 2. Therefore,
if we would choose the ratio 2, we could always keep up the ratio.
That's can a good example of practical uses of 2.
However, there is one question which still not be answered. Why 297mm*210mm of all things? Furthermore, the size of A0 is more complex: 1189mm*841mm.
The answer is the area of A0. When we calculate
the area of A0, the value is 999949mm, the approximate value of
1m2. In other words, A0 is the paper whose ratio is 2 and area
is 1m2. A1, A2, A3, A4 can be made in the process of dividing
in halve A0.
One another merit of A-Series is that we can copy a certain size
paper onto a different size paper by scaling up or down properly
since they are similar each other.