

By Soo Jin Lee and Jaehong Shin

Jay want to plant trees around the triangle lake which has sides 918m, 1170m, and 3420m as lengths. However, City Law restricts that the interval between two trees has to be regular. To minimize the expense for purchasing needed trees, at which intervals should Jay plant trees and how many trees Jay need at that time?
First, we have to find all common regular intervals
that trees can be plant regularly along all three sides. By using
spreadsheet, we can easily get those common regular, that is,
mathematically common divisors of three numbers.
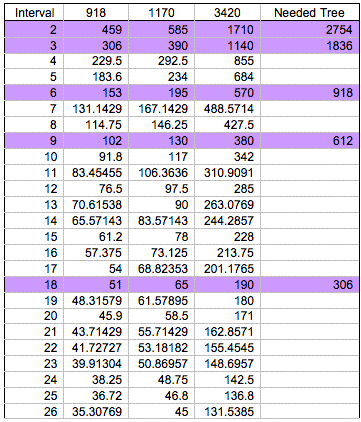
As we can see on above table, the proper interval is 18m and the number of needed trees is 306(=51+65+190) Then, more generally, given x, y, z as three sides of a triangle lake, how can we figure out set up the regular interval and needed trees?
As already shown above, first we have to consider common divisors of three numbers and find the greatest common divisor, that is, GCD of x, y, z. In order to get GCD, first we need to resolve each number into prime factors so that we can abstract all common factors from each number. After finishing the prime factoring, GCD is the interval what we want. That is,
Step 1: Resolve the length of three sides x,
y, z into prime factors
Step 2: Find GCD of three numbers as a needed regular interval.
Step 3: (x+y+z)/gcd(x,y,z) is the minimized tree number.
For example as above,
Step 1: 918 = 2 * 3 * 3 * 5 * 13
1170 = 2 * 3 * 3 * 3 * 17
3420 = 2 * 2 * 3 * 3 * 5 * 19
Step 2: GCD(918, 1170, 3420) = 2 * 3 * 3 = 18
Step 3: (918+1170+3420)/18 = 306
Now, is it Okay with everything? Does it look that simple? However, unpredicted problems can bring about esp. for secondary level students in the part which looks very easy and simple. What if three numbers would be large ones like 1160718714. Are you comfortable to factorize large numbers into primes and do you have enough energy to repeat that job?
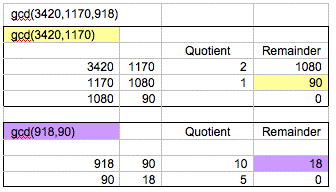
The Euclidean Algorithm is a procedure for
finding the gcd of two numbers. To explain more easily, let me
give you an example using above case.
 For Exploration, click!!
For Exploration, click!!
We could have gotten the gcd by factoring into
primes and then getting the smallest power of each prime in both
of them and multiplying together - but factoring those numbers
would not be fun. In fact if the numbers got real large, say if
they were about a hundred digits long, Ron Rivest (at MIT) conjectured
it would take 4 BILLION years to factor the numbers into primes,
while finding the gcd this way would only take a couple of months(or
less).
refer to http://mathworld.wolfram.com/EuclideanAlgorithm.html
So you see the Euclidian Algorithm is a pretty powerful thing. Now almost independent of the size of the lake, Jay can save his money without violating city's law!!