

By Soo Jin Lee and Jaehong Shin
Situation 1 : Jay would like go hunting and then go fishing for his supper meal. He decided in advance a special place for fishing but didn't for hunting. In order to save his energy for hunting and fishing, he want to find the shortest way to walk (he has no vehicle) through. Which point in forest does he have to go to so that he can save his enegy as much as possible?
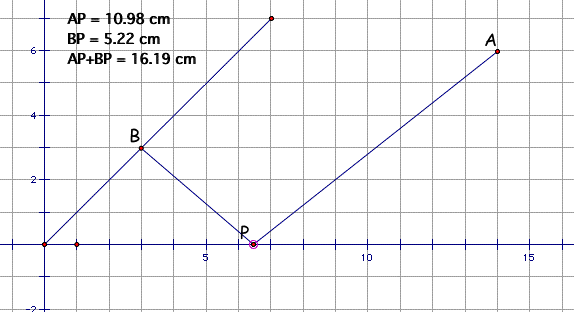
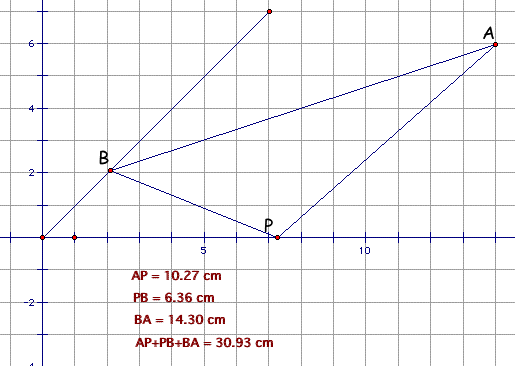
First, I restated above situation on the grid and calculate the needed distance using GSP. Let Jay's home be a point A, last place in sea be a point B, and the undecided place he have to choose at forest be a moving point P. To explore, click here.

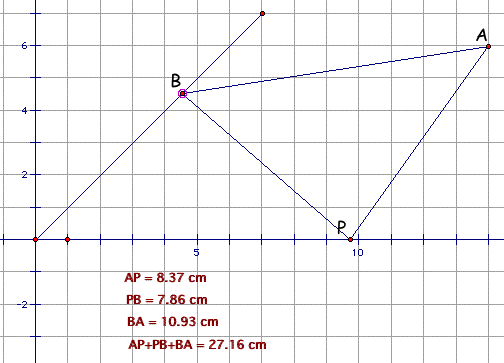
Then the problem reduce to find the minimum value of AP+BP. How can I find the minimum value? By exploring GSP, I can guess the point that makes the distance nearly to minimize as follow.
Now, let's look into more precsely and mathematicaly.
To find the point that makes the distance AP+BP shortest, dot the point B', a symmetric point of B to x-axis and connect the point A and B'. If we let the intersection of AB' and x-axis, that x-intercept be point P', the P' would be the point that satisfying above comdition since
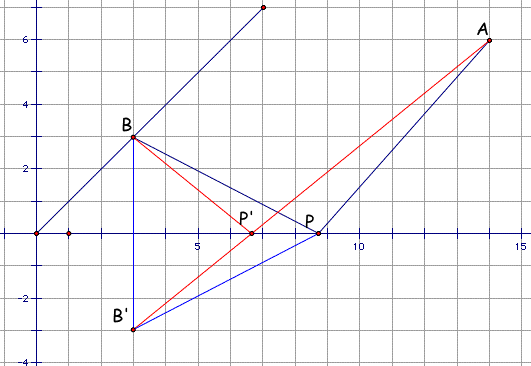
Therefore, AB' is always the shortest distance than any other paths tha could be done. Now, Jay found the point in the forest to walk (he has no vehicle) through for saving his energy!! Explore.
Situation 2 : Next day, Jay realized that he did not consider the distance to go back to home from the seashore. This time, he would like to find the shortest way including the way to home and he do not decide any particular place to drop by not only at forest but at seashore. How can you fin the shortcut for Jay?
In this time also, let Jay's home be a point A, the undecided place at sea be a point B, and the undecided one at forest be a point P. Unlike the previous situation, the movable point is two: P and B. Furthermore, just exploring the situation by GSP does not seem to work to find what we want this time because we should consider both points simultaneously. To explore click!
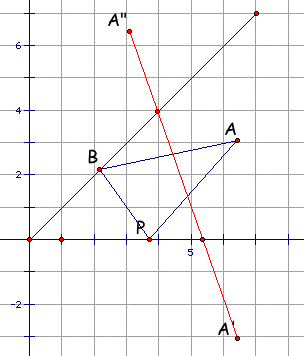
To solve the problem, let's try step by step by using the same method that we used in the first situation. First, dot the point A', a symmetric point of A to x-axis and dot the point A", a symmetric point to the seashore line(mathemacically linear function of x), and then connect the point A' and A".
Similiary, we can guess that A'A" is the shortest distance for the second situation. How can we prove it mathematically?
Let the intersection between A'A" and x-axis be a point P' and the intersection between A'A'" and the seashore line be a point B'.
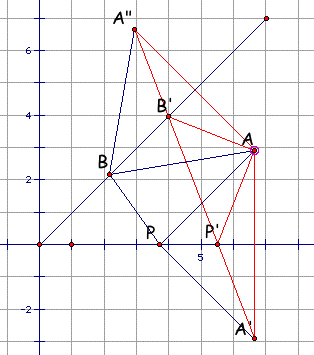
Therefore, A'A" is always the shortest distance than any other paths tha could be done. Now, Jay found the way in whic he can save his energy as least as possible although he has to go into the forest and the sea to find the reflection point!! Explore!!