

By Soo Jin Lee and Jaehong Shin
1. Number pyramid (Numerical Palindromes)
Don't you think this is amazing?
At this essay, I want to investigate the beauty of number.
Let's start our exporing from the above one.
Do you see the pattern?
First of all, number of digits of the multiplied numbers are all odd.
Since digit is odd, if we pick the middle number, each side will contain even number of digits; and those numbers are in reversed symmetrical order.
Let's see if it is really true for the infinite numbers by using EXCEL
(Chart one)
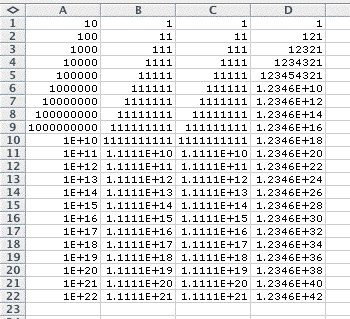
As we can see from the above, it seems true for all numbers.
Now why do you think this is true?
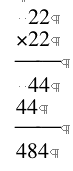
let's look at some smaller examples;
![]()
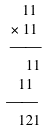
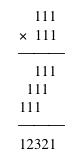
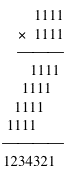

from the examples above, we can easily see the reason for the pattern.
To explain more explicitly, a 1 in a multiplier copies the multiplicand and shifts, so that the product copies the counting order of numbers -- 1, 2, 3, 4, etc. -- up to the number of ones in the multiplier, then reverses this counting order back to the starting 1.
We call this kind of numbers as "NUMERICAL PALINDROMES"
Let's look at some terms so that we can easily understand this.
Palindromic word = a string of letters whihch reads the same left to right or from right to left. ( for example, "POP", "DAD")
Palindromic sentence = a string of letters that seperate as words, left to right or right to left. Thus "Madam Im Adam" is a short Palindromic sentence.
Numerical palindromes result from squares of identity strings, that is each a string of signs all the smae, such as 111, whose square is 111 * 111.
In the DNA code for genes, a palndromic coding prevent certain kinds of errors.
What happens when we go over to 2 * 2, 22 * 22, .....?
(Chart two)
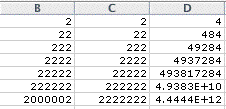
This time it is difficult to see the pattern..
In the second product above, we have 22 * 22, we have the palindrom 484, which is 4 times the correspnding case for the string 11 * 11 = 121.
The reason why it is four times the corresponding case for the string 11 * 11 is obvious.
Since 1 * 1 = 1 and 2 * 2 = 4, we can see that the square of 1 is 1 and square of 2 is 4. So 2 * 2 is obviously four times the string of 1 * 1.
Due to the same reason as the above one, it is clear to see that the answer of 22 * 22 = 484 is four times the answer of 11 * 11 = 121.
How about the third line above the chart two?
We may guess that the answer of 222 * 222 is four times the answer of 111 * 111 = 12321.
i.e 222 * 222 = 481284
But this time it is not true.
222 * 222 = 49282 and 111 * 111 = 12321.
From this line, the symmetry is broken so we can say this, as the mathematical term, the symmetry has been hidden by the decimal.
Why this will not work?
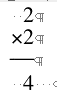
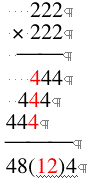
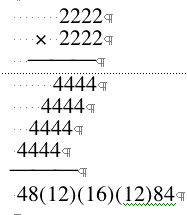
As we can see from the above calculation, except for the blackets, the remain numbers are in reversed symmetric order.
and four times the corresponding case for the square of the string 111----111 * 111 = 12321. 222 * 222 shows the way write this product in decimal languge, "49284", which is not a palindrome. That is, "the symmetry has been broken". Or, to put it another way, the symmetry has been hidden by the decimal place.
That corresponds to something discovered only in recent years in a very advanced field of physics, called "particle theory", which has a symmetry called "gauge theory". It results in "particles without mass", like the photons of light. But it has been found that, by breaking this symmetry( or hiding it) a maaless particls can acquire mass, resulting in discovery "in the laboratory" of these particles predicted by this theory! So we have modleed in artihmetic, a pattern found in physics, and a hidden pattern found in physics, along with "increase of mass"
2. Number pyramid 2
Isn't it interesting?
What made me more fascinating was the substraction between 12 and 1, 123 and 12, 1234 and 123,.....are all correspond to the answer of the right row.i.e;
From the very left part of the equation above, I could derive the right side.
Finally by observing two examples, I can conclude that number of beauty doesn't just come out by chance, although it looks very intererting for us, I believe mathematicians had spent plenty of their time to build such a beauty.