By Soo Jin Lee and Jaehong Shin
Objective: Help students compare values among rational or irrational numbers
Grade: 9
Procedure/Acitvities:
The purpose of following activities is to help students compare
among rational or irrational numbers by visualization of the each
numbers' value using GSP. Using GS, students can draw out a figure
containing all values to be compared and understand intuitively
relations among those numbers in terms of their size.
Exploration 1
First, for construction 
,
draw out a right-angled triangle which has two sides other than
hypotenuses with size 1, 2 each.
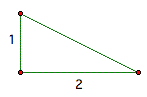By Pythagorean Theorem
Then, for construction 
,
draw out a right-angled triangle which has two sides other than
hypotenuses with size 1, 4 each.
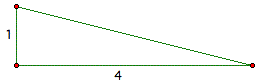By Pythagorean Theorem
Let's connect above two constructed triangles
to make a side with size 
as follows.
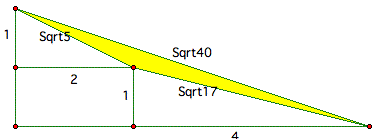By Pythagorean Theorem
Now, students can compare the sum of 
and 
with the value 
visually since one side of a triangle can
not be more than the sum of the other two sides. For exploration,
click!!
Discussion: Make
students individually compare 
with
using GSP in a similar method and
present their result of exploration.
Extension: Make students to challenge above problem without the aid of GSP and suggest an algebraical solution.
Exploration 2
There are four positive numbers satisfying following inequality.
Compare the size of following three numbers,
In a similar way to exploration 1, draw out a triangle which has two sides other than hypotenuses with size a, b and a triangle with two sides c, d each such that satisfy an assumption.
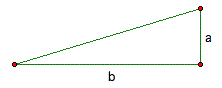
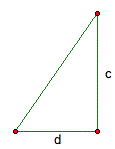
Students should have no problems in seeing that a/b < c/d since they can compare between the size of each triangle's tangent visually.
Now, to construct (a+c)/(b+d) connect two triangles properly as follows.
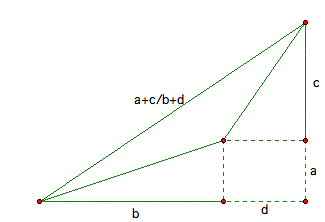For exploration,
click!!
As students can see from above drawing by comparing their tangents one aother, the size of (a+c)/(b+d) is the middle of the size of a/b and c/d. that is,
Extension : Make students to be aware that they can not solve comparison problems by drawing method and lead to an algebraical method.
Ex) (a+c)/(b+d) a/b -> (bc-ad)/b*(b+d) > 0 (Because bc-ad>0 by assumption)
Therefore, (a+c)/(b+d) > a/b