

By Soo Jin Lee and Jaehong shin
Day 1
Can you see why the below infinite series come out with the finite number "1/3"?
1/4 + (1/4)^2 + (1/4)^3 + (1/4)^4 + ... + (1/4)^n + ... = 1/3
Before we investigate our answer about the above question, let's first learn some notions.
we called the above equation " Infinite Geometric" series in mathematical term.
Infinite, because it has an infinite number of terms,
Geometric, because the ratio of any two consecutive terms is constant.
It may be that you've never encountered the notion that an infinite series could have a finite sum.
That is a very odd and intriguing idea. It seems that if you kept addinf to the series long enough, it would eventually increase without bound, and the sum would go to infinity. But that's not the case.
Since we now understand some concepts, let's further our study to investigate the question.
We will use visualising to approach the answer.
(mention the importance of visualizing here...)
1. How can we show a visual representation of an infinite series of the question?
(A) Let's look at this isosceles trapezoid.
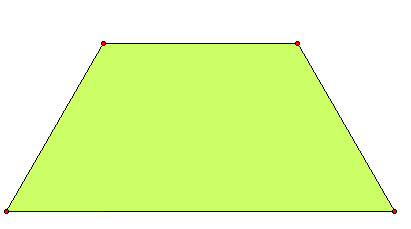 (consider this whole
colored area "1")
(consider this whole
colored area "1")
(B) you can divide it into 4 smaller trapezoids, each with an area 1/4 the original.
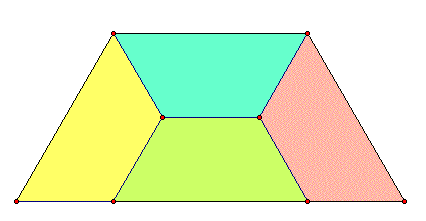
we'll focus on the yellow trapezoid.
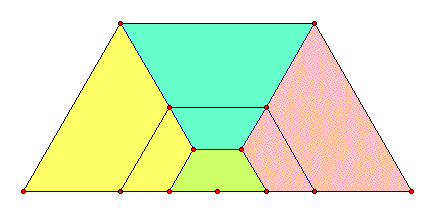
(C) Here is the original yellow trapezoid, which is 1/4 of the green trapezoid in (A), plus a smaller yellow trapezoid that is 1/4 of the green trapezoid in (B). The smaller yellow trapezoid is 1/4 of 1/4, or (1/4)^2.
(Remember that to find 1/4 of 1/4 we multiply 1/4 * 1/4, and a number multiplied by itself is squared.)
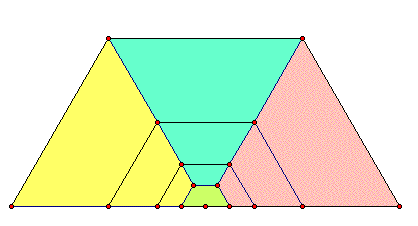
(D) Now we have the original yellow trapezoid, 1/4 of (A), plus the smaller yellow trapezoid from (B)(1/4 of 1/4), plus an even smaller yellow trapezoid that is 1/4 of the green trapezoid in (C). That makes 1/4 of 1/4 of 1/4, or....(1/4)^3.
(Remeber that a number multiplied by itself twice is cubed.)
(Question 1)
Try to contsruct (A) to (D) by yourself, then constuct some more like (1/4)^4, (1/4)^5..
(Question 2) What will be the answer for,
1/4 + (1/4)^2 + (1/4)^3 + ... + (1/4)^n +... =?
this notation means that we will be repeating this process infinitely many times.
hint> Look at the figures above, and try to derive what fraction of the total figure will be yellow.