FINAL ASSIGNMENT

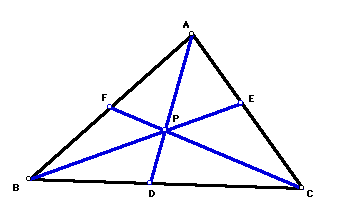
A. Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

By using GSP, let's first draw an arbitrary triangle having conditions as mentioned at question.

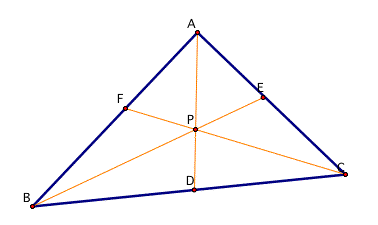
To find any connectioon between (AF)(BD)(EC) and (FB)(DC)(EA),

I calculate each segments' length and multiply.

Interestingly, those two multiplications come out same result.

so I guess (AD)(BD)(EC) = (FB)(DC)(EA). ( to see it always satisfied, click here to see GSP tool)

*** For Various Triangles ***

1) an isosceles triangle

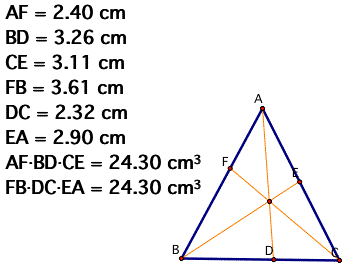
2) a right triangle

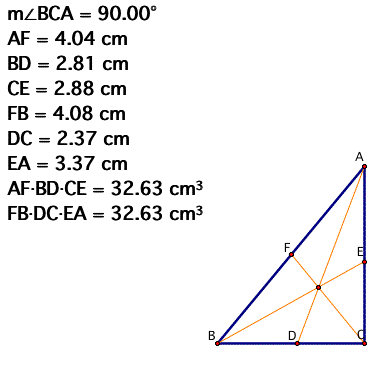
3) an equilateral triangle

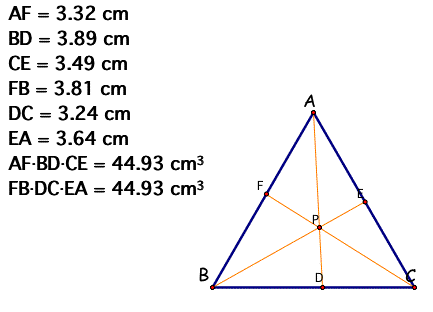
*** let's move around the point P!!! ***

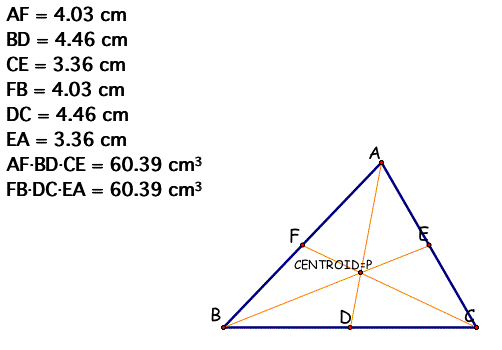
When P is a Centroid,

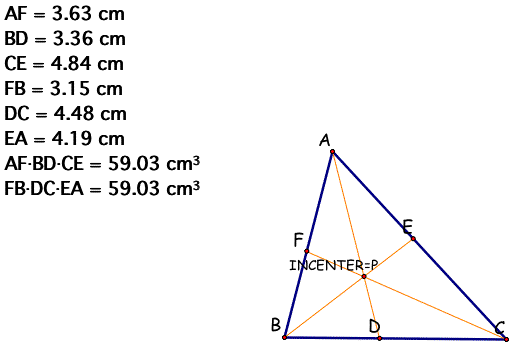
When P is an Incenter,

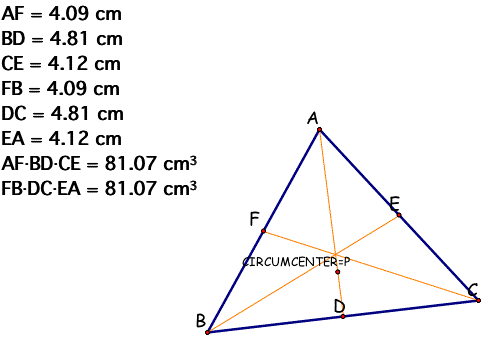
When P is a Circumcenter,

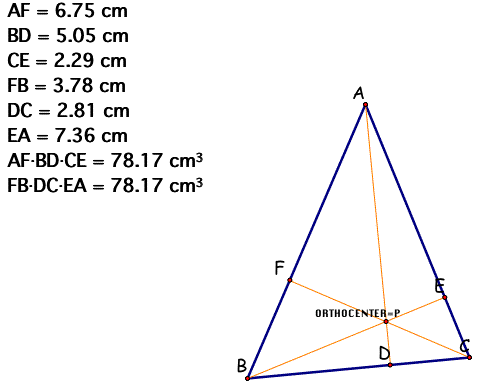
When P is a Orthocenter,

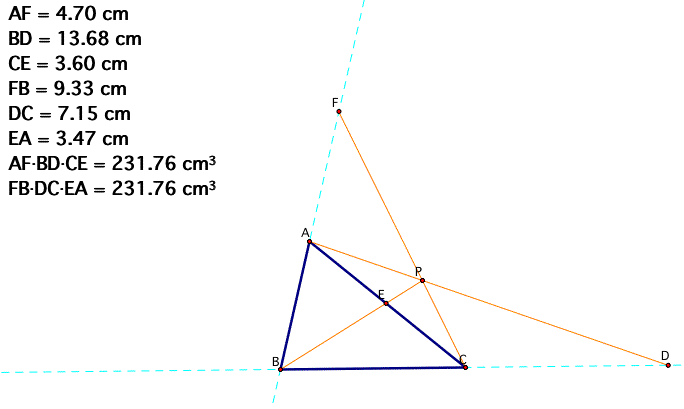
When P is at the outside of the triangle,

B. Conjecture? Prove it! (you may need draw some parallel lines to produce some similar triangles) Also, it probably helps to consider the ratio

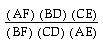
Can the result be generalized (using lines rather than segments to construct ABC) so that point P can be outside the triangle? Show a working GSP sketch.

As I conjectured at A,
(AD)(BD)(EC) = (FB)(DC)(EA) always satisfied for any triangles and any locations of P.

To prove the theory, I will draw some parallel lines to produce some similar triangles.

First draw a parallel line which is parallel to the line BC,

 

By drawing only one line will give us many useful equalities to utilize.

The equalities will come from similar triangles...

As looking at the colored triangles APH & CPD,

we can easily notice those two triangles are similar to each other.

< APH = < CPD,

< AHP = < PCD,

< PAH = < CDP.

Since all three angles are same, triangle APH is similar to CPD.

from that, we will get this ratio; (AH)/(CD) = (AP)/(DP) = (HP)/(CP)-----------------#

 

Next we can also look through these similar triangles,

Since < APG = < BPD,

< PAG = <PDB,

< PBD = <PGA,

tirangle APD & BPD are having similarity.

From this, we will get the ratio; (DP)/(AP) = (BP)/(GP) = (BD)/(AG)----------------##

 

We can also look at this case;

Since < AFH = < BFC,

<HAF = < BCF,

< AHF = < BCF,

triangle AHF is similar to the triangle BFC.

Hence, (AF)/(BF) = (FH)/(CF) = (AH)/(BC)-----------###

The last case we should consider is as below;

Since < AGE = < EBC,

< EAG = < BCE,

< AEG =< BEC,

triangle AEG & BEC is similar to each other.

Thus, we will get the ratio, (CE)/(AE) = (CB)/(AG) = (EB)/(EG)-------####

 

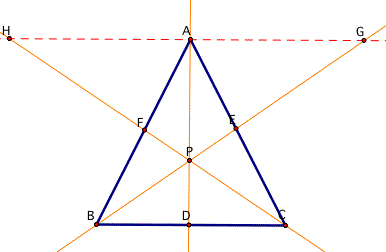
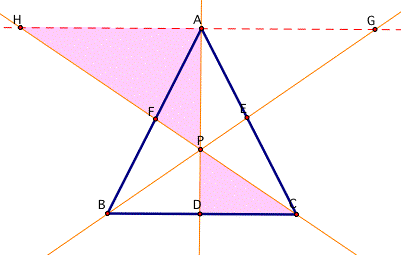
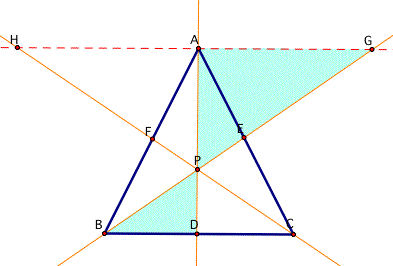
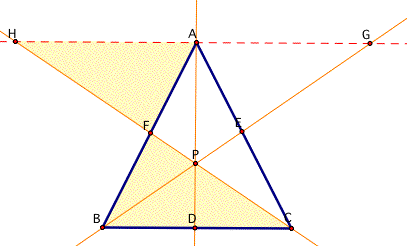
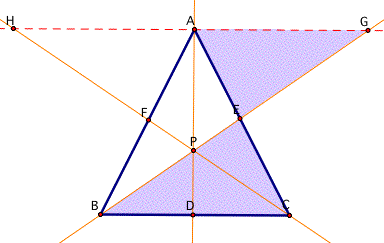
Now let's think about

------------*,

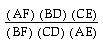By using ###((AF)/(BF) = (FH)/(CF) = (AH)/(BC)), ####((CE)/(AE) = (CB)/(AG) = (EB)/(EG))

Substitute (AH)/(BC) instead of (AF)/(BF), and (CB)/(AG) instead of (CE)/(AE) .

Then we will get the equation as this;

(AH)(BD)(CB)/(BC)(CD)(AG).

By cancelling out same factor (BC), (AH)(BD)/(CD)(AG) is left.

Then let's subtitute (DP)/(AP) instead of (BD)/(AG), and (AP)/(DP) instead of (AH)/(CD).

Likewise, by cancelling out, (DP)(AP)/(AP)(DP) is 1.

Thus, 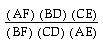= 1 ;

(AF)(BD)(CE) = (BF)(CD)(AE) is proved.

C. Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?


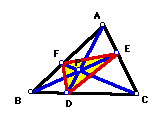
Let's see the picture below,

 

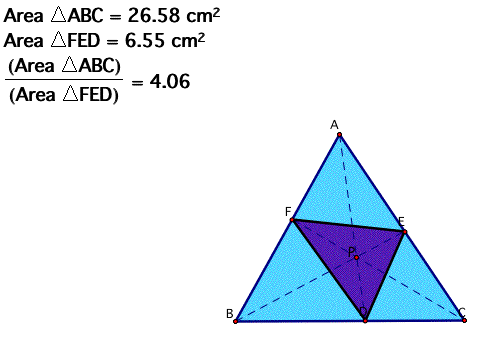
We can easily see through the result I got from the triangle ABC; area of the triangle ABC is greater than the are of the inner triangle DEF.

 

Let's find the case when the area of ABC is exaclty 4 times the area of EFC.

Concider that the point P is centroid,

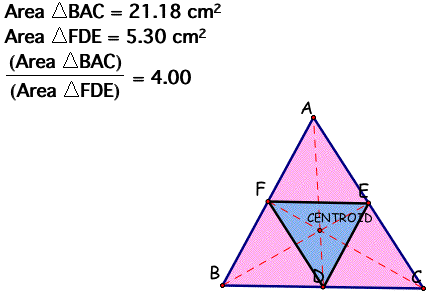
Now, it is obvious to see that the area of the triangle ABC is exactly 4 times larger than the triangle DEF.

 

When point P is a centroid, segment EF and BG is parallel, so the length EF is 1/2 of the length BC.

So the area of 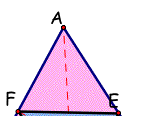is 1/4th of the original triangle,

since 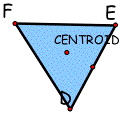and is having same area,

as a result, tringle ABC = 4 * DEF.

Return to my homepage~~~