

Why do we have divisibility tests?
Divisibility tests tell us if one counting number is divisible by another counting number without actually carrying out the division. We will see other uses for divisibility tests after we learn the tests and see why they work.
Rules:
Divisibility Test for 2:
If a number, n, is divisible by 2, then the last digit of n is divisible by 2.
Example: Is 2358492658 divisible by 2?
Answer: yes, because the last digit, 8 is divisible by 2.
Divisibility Test for 3:
If a number, n, is divisible by 3, then the sum of the digits of n is divisible by 3.
Example: Is 3425796372 divisible by 3?
Answer: First add the digits of the number, 3+4+2+5+7+9+6+3+7+2=48. Then check to see if 48 is divisible by 3?
Again add the digits of the number 48 and you get 4+8=12. Since 12 is divisible by 3, our original number is divisible by 3.
Divisibility Test for 4:
If a number, n, is divisible by 4, then the last two digits of n must be divisible by 4.
Example: Is 54238756824 divisible by 4?
Answer: Since 24 is divisible by 4, then our original number is also divisible by 4
Divisibility Test for 5:
If a number, n, is divisible by 5, then the last digit of n is either a 0 or a 5.
Example: Is 56248976230 divisible by 5?
Answer: Yes, because the last digit of the number is 0.
Divisibility Test for 6:
If a number, n, is divisible by 6, then it must pass the divisibility test for 2 and 3.
Divisibility Test for 7:
If a number, n, is divisible by 7, then take the last digit off the number n and call that new number r. Next, double the last digit that you took off and subtract the doubled number from r. If that new number is divisible by 7, then the original number n is also divisible by 7.
Example: Is 408548 divisible by 7?
Answer: 40854-16= 40838
4083-16=4067
406-14=392
39-4=35 and yes 35 is divisible by 7.
Divisibility Test for 8:
If a number, n, is divisible by 8, then the last three digits of n must be divisible by 8.
Example: Is 5634585104 divisible by 8?
Answer: Since 104 is divisible by 8, then our original number is also divisible by 8.
Divisibility Test for 9:
If a number, n, is divisible by 9, then the sum of the digits of n also are divisible by 9.
Example: Is 72386190 divisible by 9?
Answer: Yes, because the sum of the digits, 7+2+3+8+6+1+9+0=36, and 36 is divisible by 9.
Divisibility Test for 10:
If a number, n, is divisible by 10, then the last digit of n will be 0.
Example: Is 25687430 divisible by 10?
Answer: Yes, because the last digit is 0.
Why do divisibility test work?
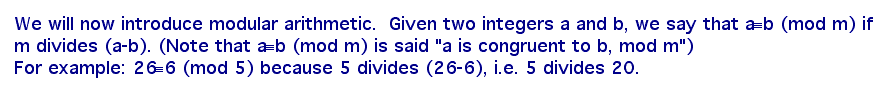

Proof of the Divisibility Test for 3:

Proof of the Divisibility Tests for 9:


Uses for Divisibility Tests
Now that you have learned the divisibility tests for 2,3. . . 10 and seen why the divisibility tests work, we will learn some practical uses of the tests. We can use the divisibility tests as a short-cut to check and see if a large number is divisible by a smaller number; however, they do have real-world usefulness.
History: Before calculators and computers the addition of many numbers was a time consuming process. Accountants needed a method to check and see if their arithmetic was correct without adding the numbers up a second time. They used a method called "Casting out Nines" that uses the divisibility test for 9.
Example of Casting out Nines:
An accountant has six numbers and he adds the numbers up quickly. Use the idea of casting out nines to check and see if his arithmetic is correct.

Now Add digits of 269=2+6+9=17
Now check that 9/53-17
and since 9/36, we know that our original arithmetic of 269 was correct.