Area of a Rectangle:

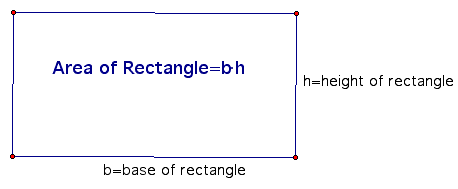
Recall that the diagonal of a rectangle divides the rectangle into two equal parts:

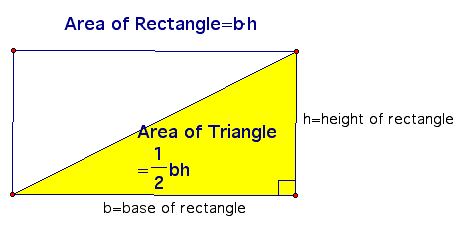
Area of a Right Triangle:

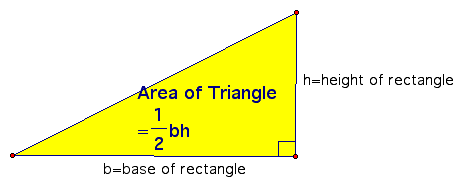
Does this equation still work for an obtuse triangle?

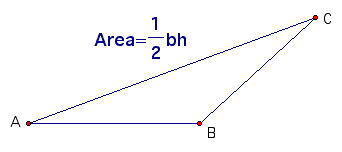
In the above triangle, what would be the base and what would be the height, because we do not have a side of the triangle that is perpendicular to another side of the triangle.

Now we will use Cavalieri's Principle about Shearing and GSP to explore this:

Cavalieri's Principle for area:

This principle says that when you shear a triangle, the area of the original triangle and the sheared triangle are equal.

Definition of Shearing:

1. When shearing a triangle, each point moves along a line that is parallel to the fixed side. So we will fix AB and shear point C along a parallel line to AB.

2. When shearing, segment AC remains the same distance away from BC as in the original triangle.

3. Shearing does not change the height of the triangle. If you drew a perpendicular line from point C to base AB, this height will not change when you shear.

If you follow these rules for shearing, you can shear Triangle ABC into a right triangle and you will see that the formula for the area of an obtuse triangle is the same as the area of a right triangle. You will also see what the base and the height of the obtuse triangle will be.

Click here to open GSP and follow the instructions for shearing the triangle. Below you can see what is in the GSP attachment.

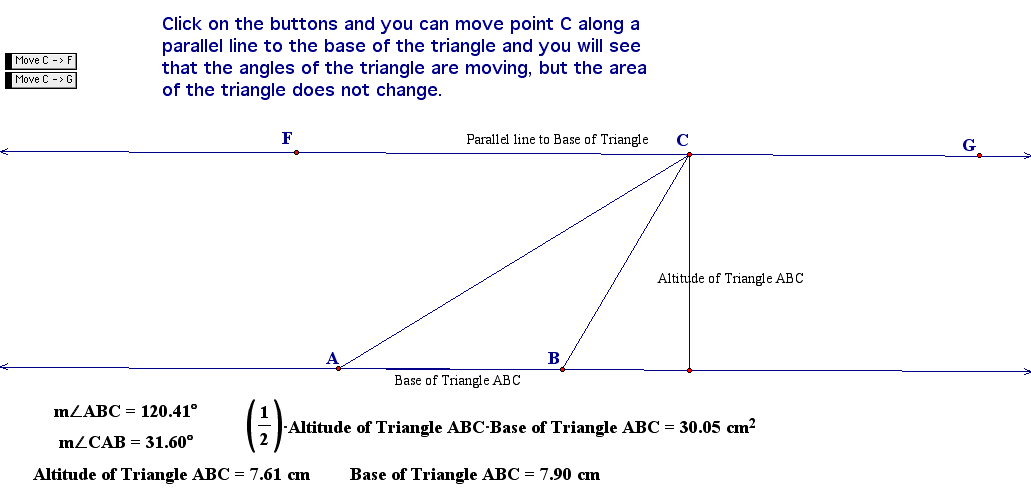
As you have just observed, the area of triangle ABC does not change when we follow the shearing rules, so let's use what we have just learned and find the area of our obtuse triangle ABC in the earlier example.

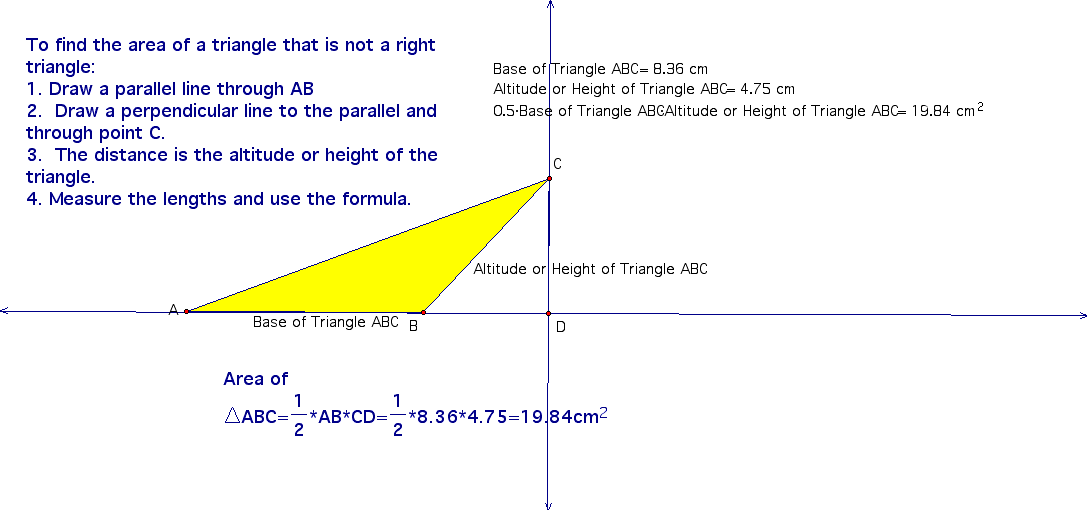
Conclusion: The formula for the area of a right triangle works for all TRIANGLES!

Return to Nikki's 6690 Website

Return to Brook's 6690 Website

References:

Beckmann, Sybilla. Mathematics For Elementary Teachers. New York, NY: Pearson, Addison Wesley, 2005.