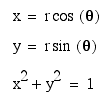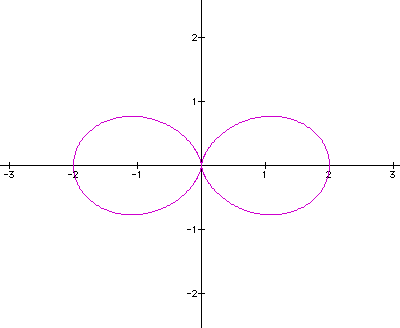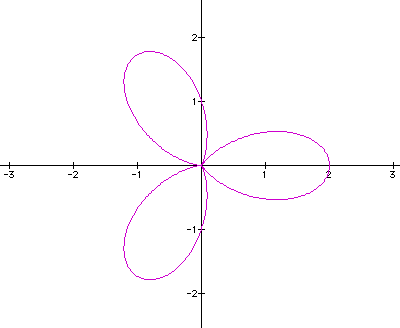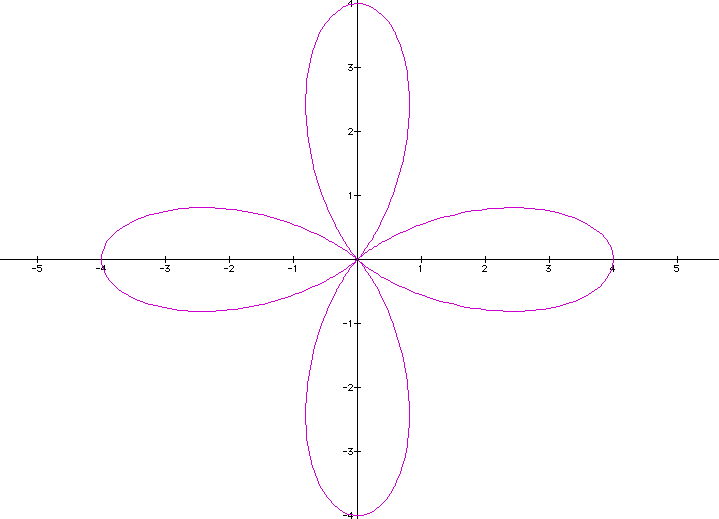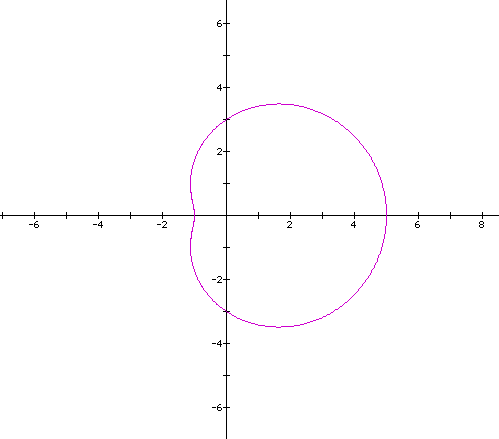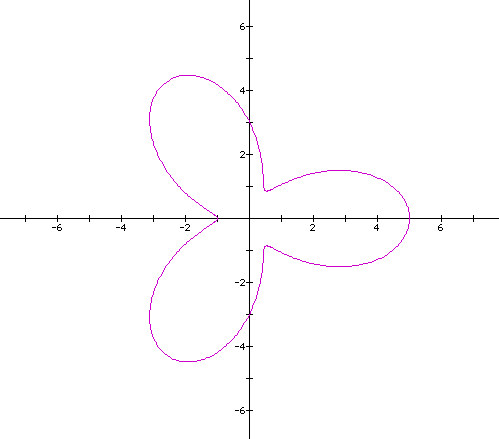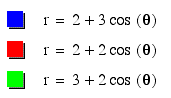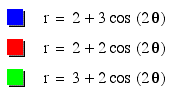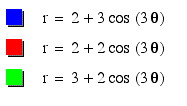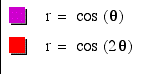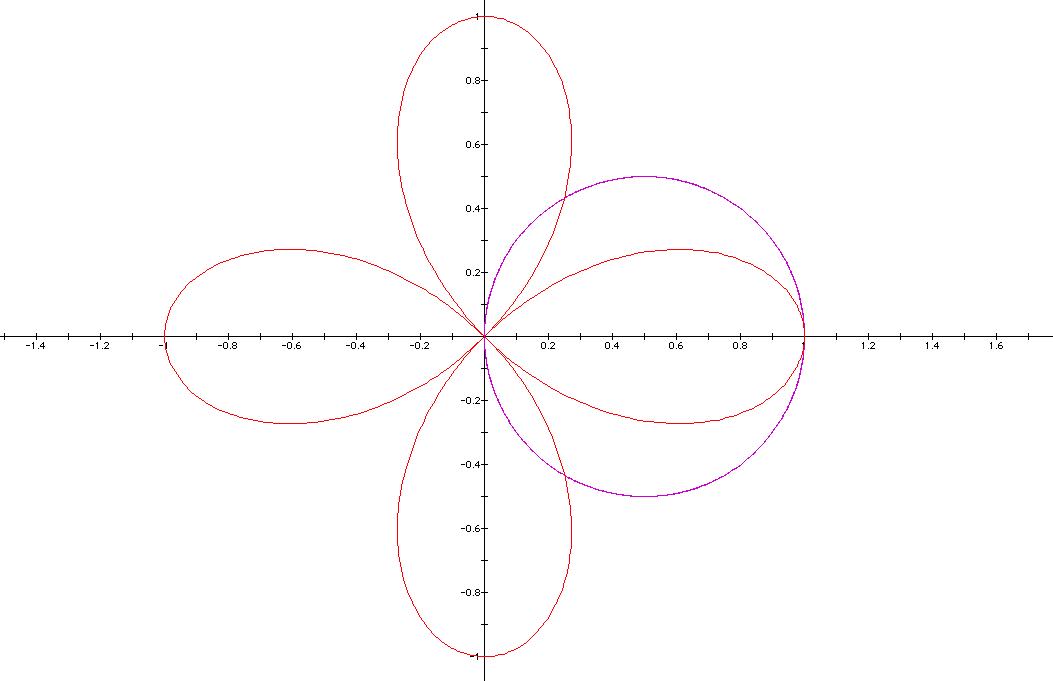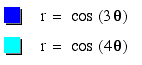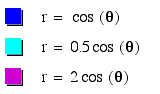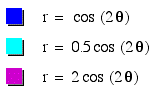Assignment #11

By Nikki Masson

Polar Equations

Review:

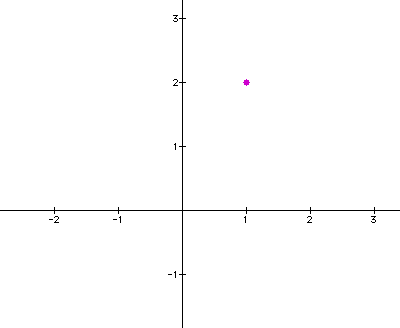
Recall that we define a point (x,y) on the plane as x units to the right of the origin and y units to the left of the origin. Below is a graph of the point (1,2).

This works great for lines and parabolas, but now we are going to graph more complex figures using polar coordinates.

Definition of Polar Coordinates: Now a point will be given as such: (r, theta). This r is the distance from the origin to the point and the second coordinate, theta, is the angle that the vector from the origin to the point makes with the positive x-axis. To convert cartesian equations to polar equations use the following rules:

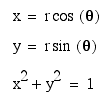
Investigation into Polar Equations

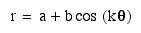
We are going to be exploring the above polar equation for different values of a, b and k and see how the values affect the graph.

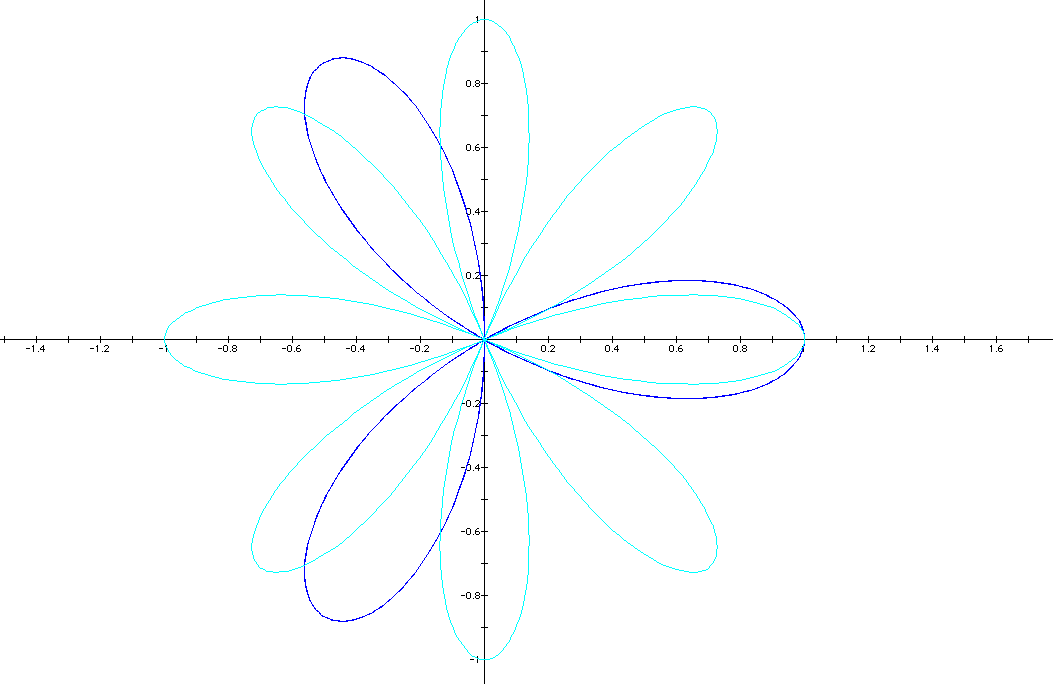
Part I : A=B and k is an integer that will vary:

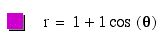
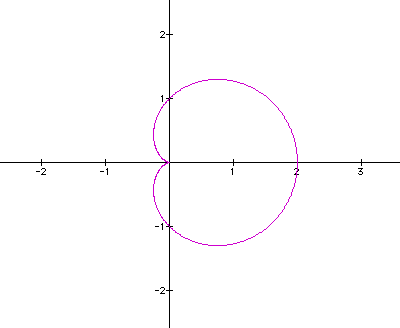
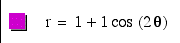
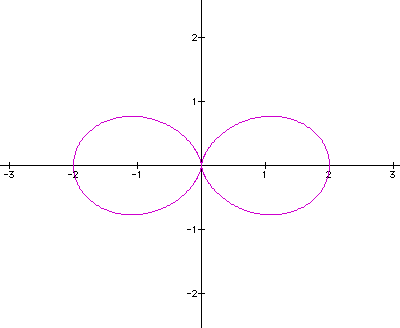
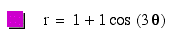
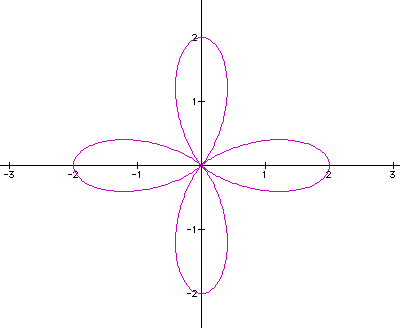
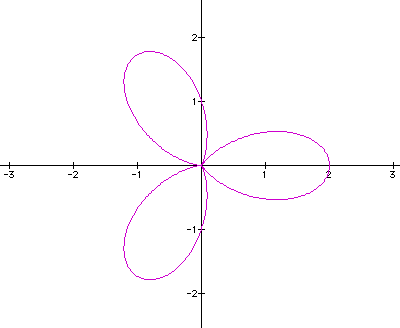What seems to be the pattern here? As k increases, the number of "leaves in the flower increases"? If we increase k=4, we should get four "leaves."

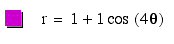
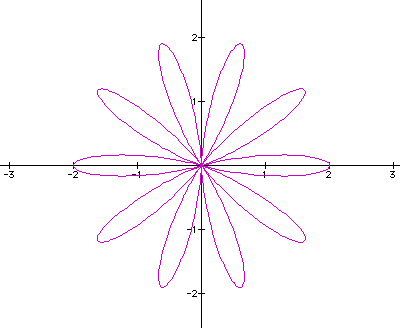
Let's look at k=10 and see if we the pattern still works.

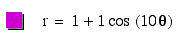
In all the above graphs, A=B=1 and k varied. What if A=B=5, would k still be the numbe of leaves?

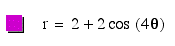
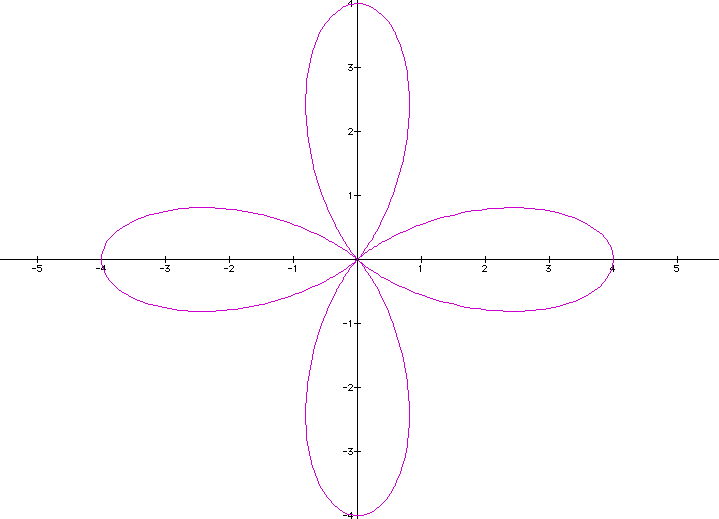If you compare the above equation to the equation earlier equation with four leaves, you will see that as you increase a=b, the graph becomes "leaves" become larger.

Conclusion: When A=B, then k= the number of "leaves in the flower."

Part II : A>B and k is an integer that will vary:

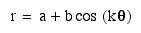
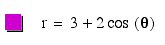
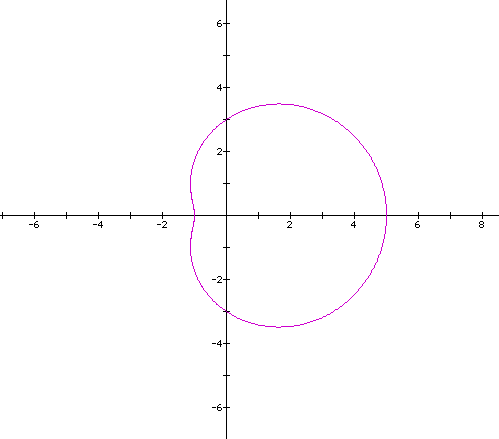This graph looks very similar to the above when k=1 and a=b, let's keep investigating and see if a>b has an impact on the graph.

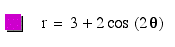
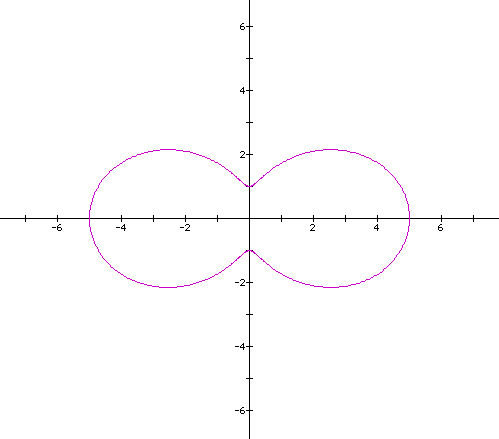Now, the leaves are not meeting in the middle, let's keeping investigating:

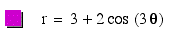
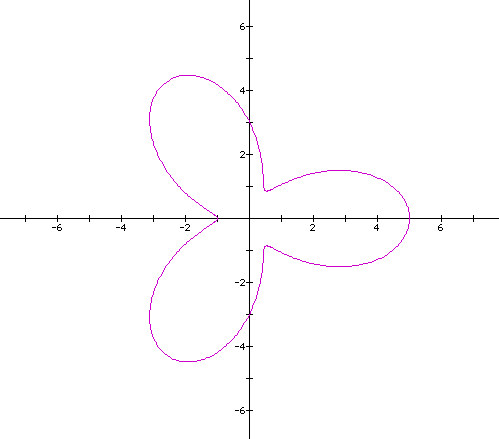
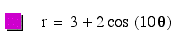
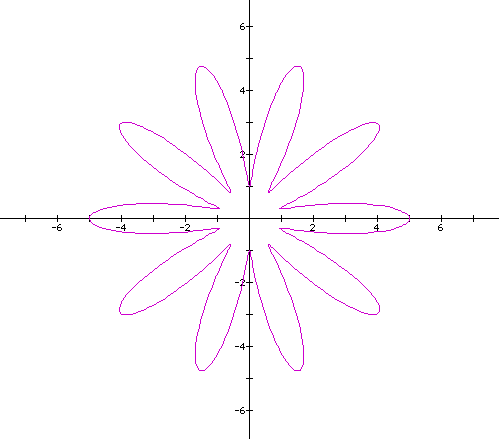As, we can see, when a>b, the leaves do not meet at the origin as they did when a=b. In all the above polar equations for part II, a=3 and b=2. Let's see what happens when a=4 and b=2.

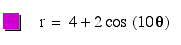
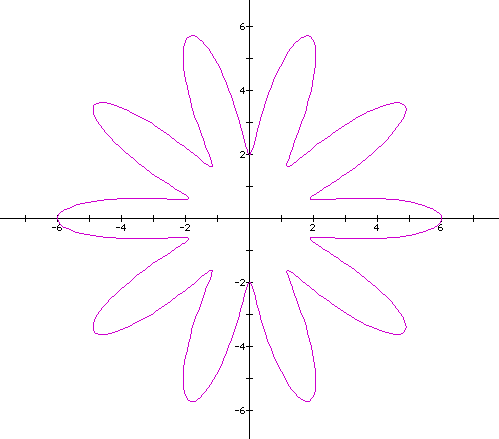Conclusion: In comparing the two above equations we see that as the difference from a to b gets larger, the leaves meet further and further away from the origin.

Part III : A<B and k is an integer that will vary:

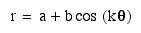
To help us better compare how a and b are affecting the graphs, I will draw three graphs on each picture, the new graphs when a<b will be in blue.

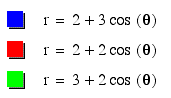
The blue curve has one loop at the origin when k=1. When we increase k=2, let's see what happens:

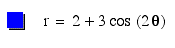
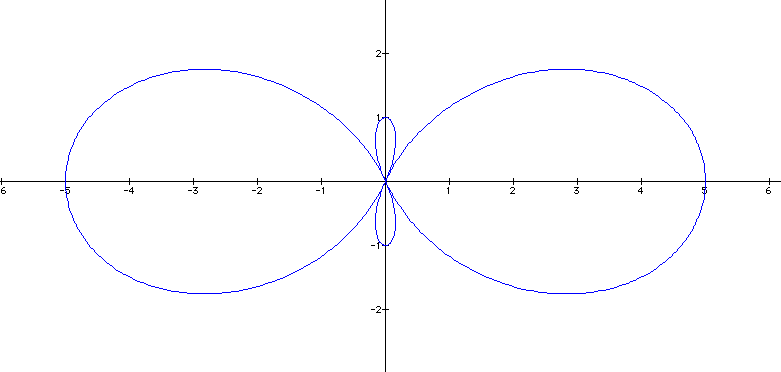Now, we see two extra loops when k=2. Let's compare the above graph with a couple more that we have already seen:

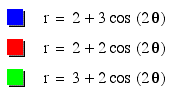
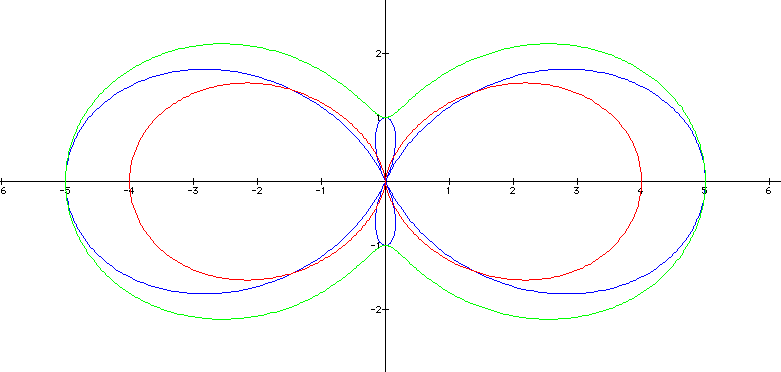
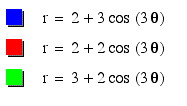
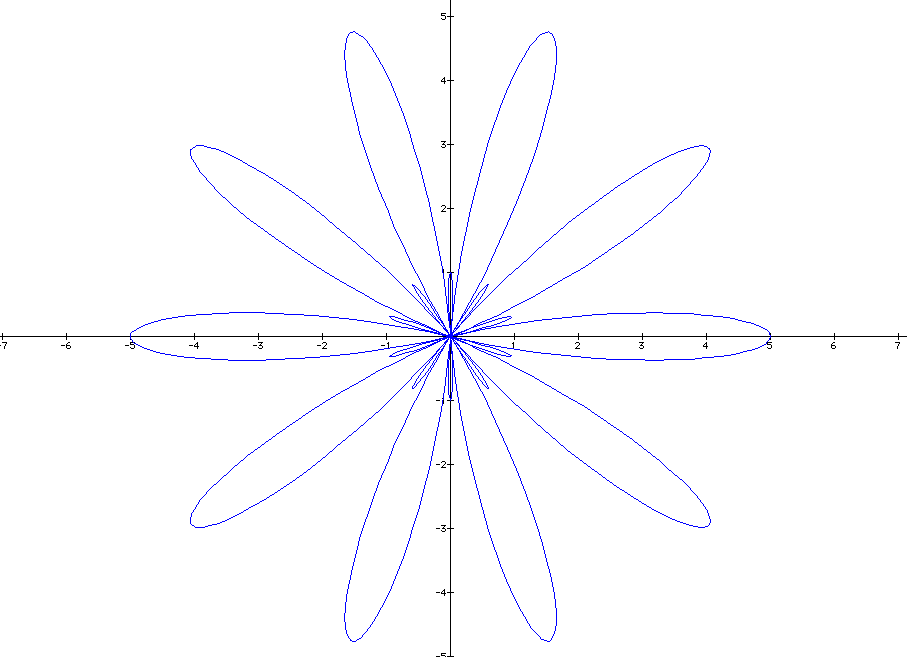
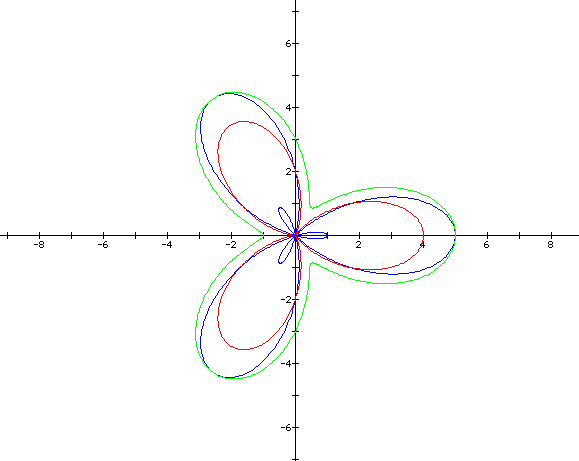What do we expect for k=10, when a<b? From the above patterns, the graph will look just like the graph when a=b, but there will be 10 extra loops inside the larger loops or "leaves".

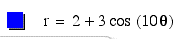
Part IV : Investigate

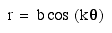
Part A: b=1 and k varies

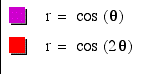
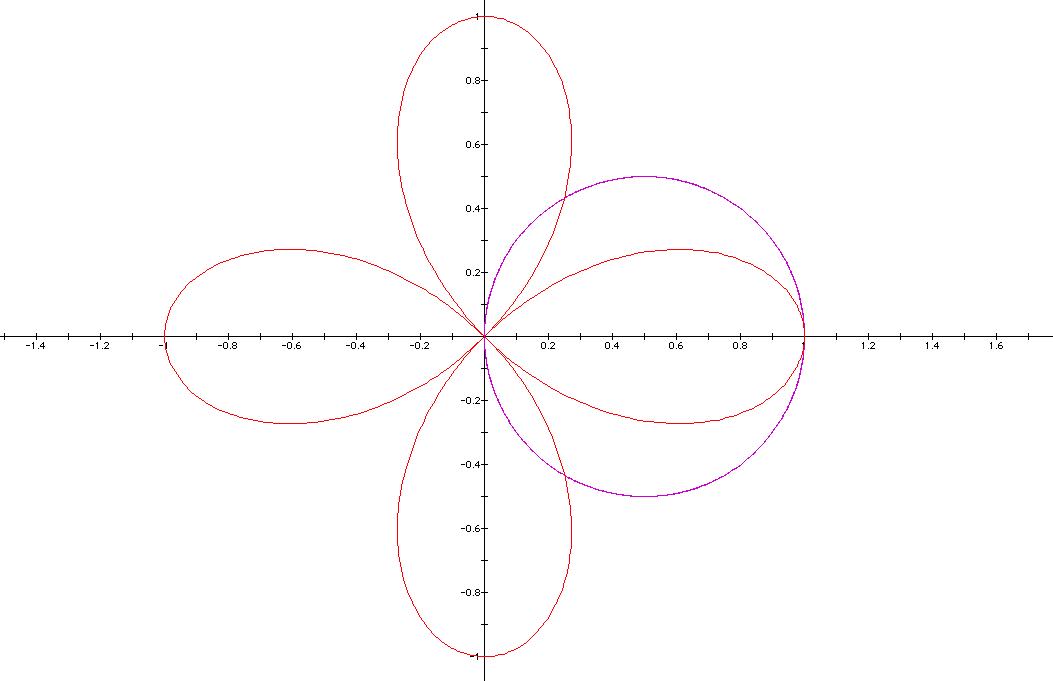
Part A: b varies and k=1

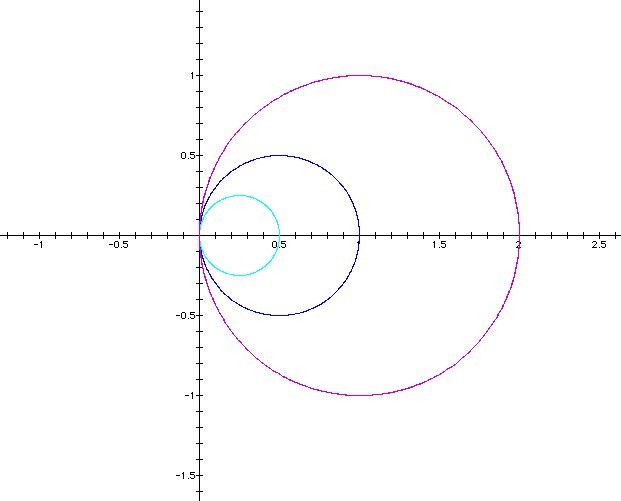
You can continue investigating polar equations in Graphing Calculator 3.2 or TI-83 and similar calculators.

Suggestions would be to change cos to sin and investigate as we have just done.

 

Return