

Part 1: Varying values of a
First we will look at the graph when a varies, but b and c are held constant. To better understand how a affects the graph, let us look at the following graphs for different values of a, when b and c are held constant at b=0 and c=0.
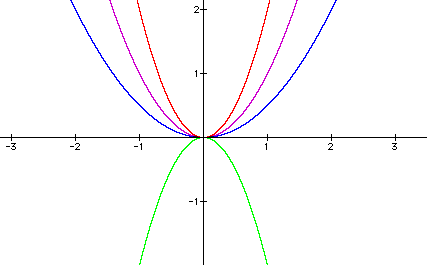
As we can see from the above graph, positive values of a either shrink or stretch the parabola. Notice that for postive values of a, as a increases, the graph shrinks but when a decreases the graph stretches. When a is a negative number the graph is reflected over the x-axis or it changes direction.
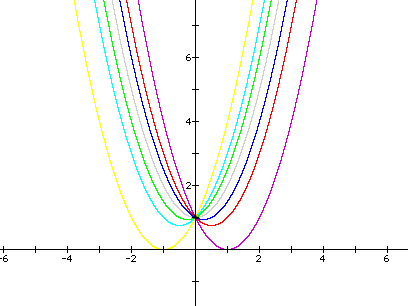
Now let us look us explore the graph when a varies and b and c are held constant at b=c=1.
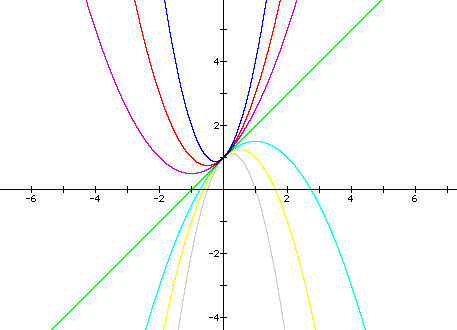
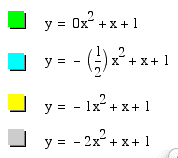
As you can see from the above graph, the different positive values of a give us concave up parabolas and the negative values of a give us a concave down parabola. When a=0, the equation become y=x+1 (shown in green) and we no longer have a parabola, but a straight line through the point (0,1). You can also observe that all of the graphs no matter what the value of a is go through the point (0,1).
Part 2: Varying values of b
Now let us explore the equation for different values of b. We will hold a and c constant at a=c=0, so
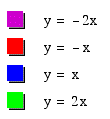
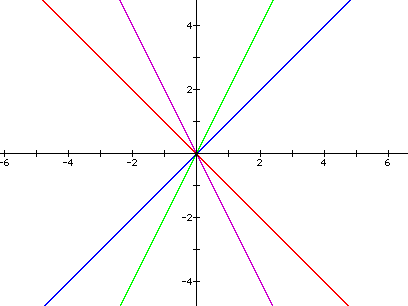
When a and c are 0, we get a linear equation, which is a line through the origin. When b is positive, the slope of the line is positive and as b gets larger, the line becomes steeper. When b is negative, the slope of the line is negative and as b gets smaller the line becomes steeper.
Now we will look at an another example, when b varies and a=c=1.
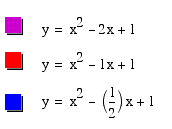
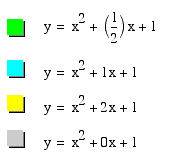
Now we are back to exploring a parabola, when a=c=1. As you can see from the graph, all of the equations go through the same point (0,1). As the positive value of b increases, the parabola shifts to the left and becomes wider. As the negative values of b decrease the parabola shifts to the right and also becomes wider.
Part 3: Varying values of c
Now let us explore the equation for different values of c. If we hold a and b constant at a=b=0, then we get y=c, which is just a vertical line that shifts up and down depending on the value of c.
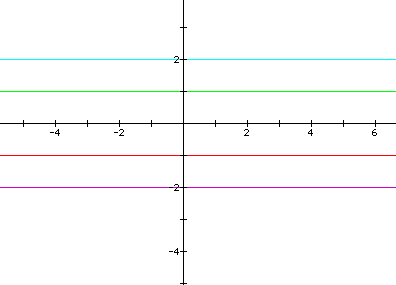
Now we would expect that the value of c would just shift our parabola in the positive or negative vertical directions. Let's examine this by setting a=c=1, for different values of c.
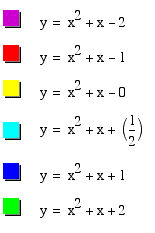
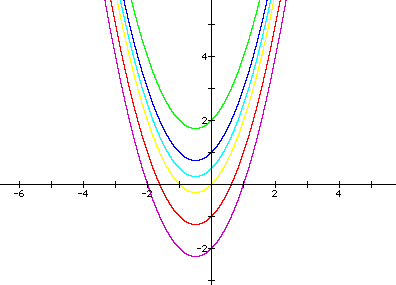
Our conclusion was right, as c increases the parabola just shifts up the vertical axis.