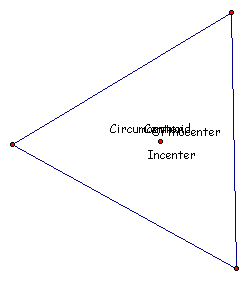
In this exercise we will explore the centers of triangles using GSP. First let us do a quick review of some definitions.
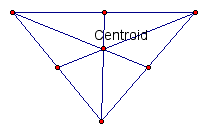
Centroid
The CENTROID (G) of a triangle is the common intersection of the three medians.
Orthocenter
The ORTHOCENTER (H) of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side.

Circumcenter
The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. The circumcircle is the circle created by the vertices of the triangles and the circumcenter as the center.

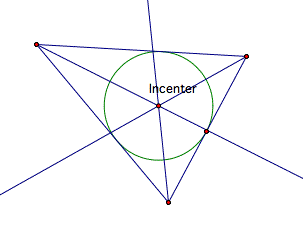
Incenter
The INCENTER (I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides.
Now that we have reviewed some of the definitions for the different centers of triangles, we will do some exploration into how these four different points change when the triangle is obtuse, acute, or right.
Acute Triangle

For an acute triangle, we see that all four of the different centers are located inside of the triangle. Next, we will look at a right triangle:
Right Triangle

From the above picture, we can see that when we have a right triangle, the orthocenter is directly on top of the the vertex and the circumcenter is on the oppositie side of the triangle.
Obtuse Triangle

For an obstuse triangle, the orthocenter and the circumcenter are now outside of the triangle and the only two points inside the triangle are the centroid and the incenter.
If we look back at the three different triangles, it seems that the orthocenter, centroid, and circumcenter all form a line. Next, we will explore this: