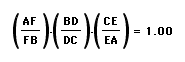Final
Assignment
By
Nikki Masson
Final
Assignment
By
Nikki Masson
Part
I:
Consider any
triangle ABC. Select a point P inside the triangle and draw lines
AP, BP, and CP extended to their intersections with the opposite
sides in points D, E, and F respectively.
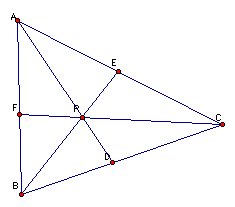 Now move
the point P around and explore the lengths of AF, BD, CE, EA,
FB, and DC.
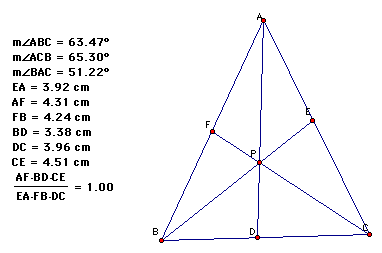
A. Calculate:
Now move
the point P around and explore the lengths of AF, BD, CE, EA,
FB, and DC.
A. Calculate:
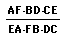
 B. Move
the point P and calculate the same relationship:
B. Move
the point P and calculate the same relationship:
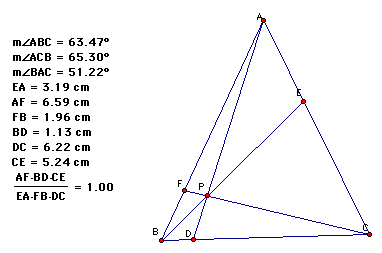 C. Move
the point P one more time and again calculate the relationship:
C. Move
the point P one more time and again calculate the relationship:
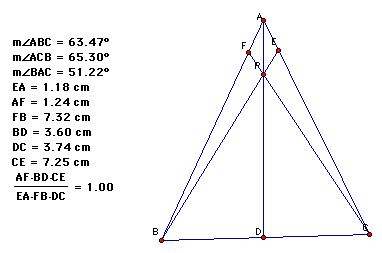 Conjecture:
When P is inside the triangle the relationship (AF*BD*CE)/(EA*FB*DC)=1.
Conjecture:
When P is inside the triangle the relationship (AF*BD*CE)/(EA*FB*DC)=1.
Part
II:
Now we will
prove the conjecture we just made.
This conjecture
we just made is called Ceva's Thoerem and
it states that:
If the
points F, D and E are on the sides AB, BC and AC of a triangle
then the lines AD, BE and CF are concurrent if and only if the
product of the ratios
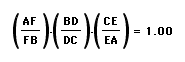
Proof:
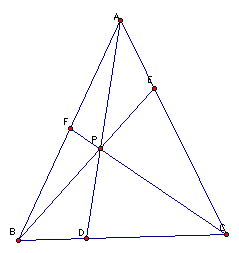
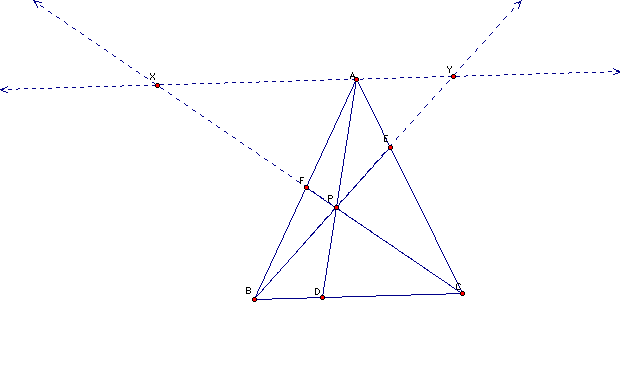
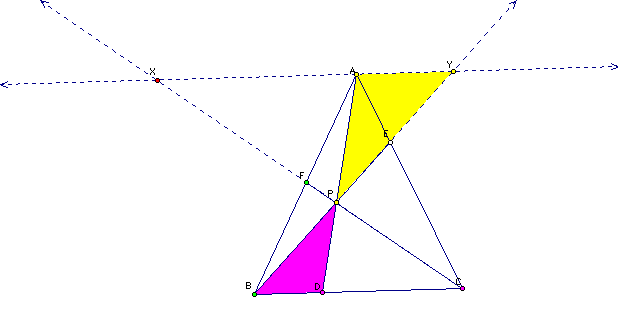
1.) Extend
the lines BE and CF beyond the triangle and draw a line through
A and parallel to BC. Mark the points where the the extended lines
cross the parallel line.
2.) There
are several pairs of similiar triangles which give us the following
ratios:
a.)
EBC and EAY are similiar triangles
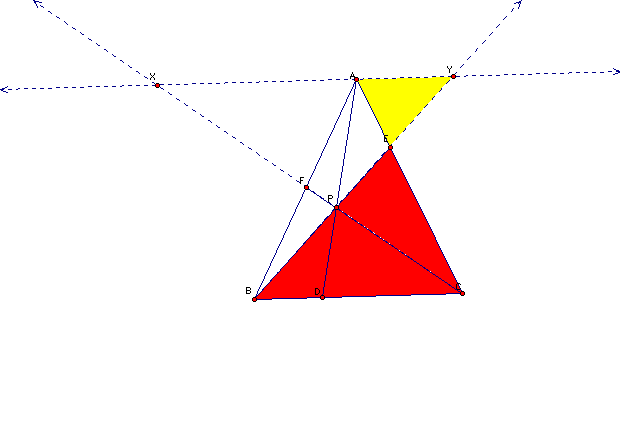 So
we get the ratio: (EC/EA)=(BC/YA)
b.
FBC and FAX are similiar triangles
So
we get the ratio: (EC/EA)=(BC/YA)
b.
FBC and FAX are similiar triangles
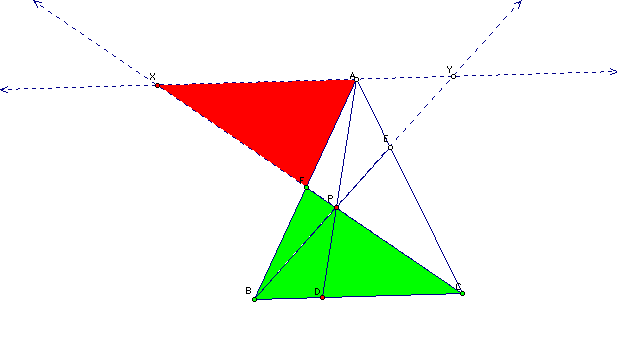 So
we get the ratio: (FA/FB)=(AX/BC)
c.
XAP and CDP are similiar triangles
So
we get the ratio: (FA/FB)=(AX/BC)
c.
XAP and CDP are similiar triangles
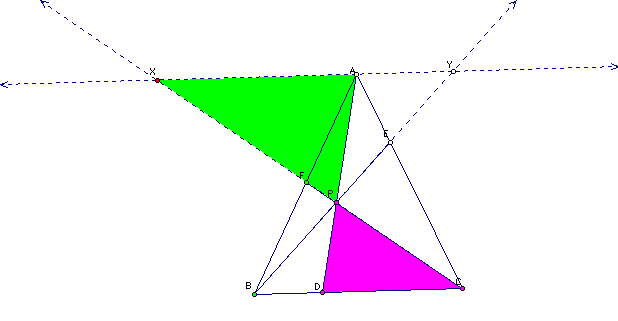 So
we get the ratio: (XA/CD)=(PA/PD)
d.
BDP and YAP are similiar triangles
So
we get the ratio: (XA/CD)=(PA/PD)
d.
BDP and YAP are similiar triangles
 So
we get the ratio: (BD/YA)=(PD/PA)
If
we mulitply the ratios together, we get:
(BD/YA)*(XA/CD)*(EC/EA)*(FA/FB)=(PD/PA)*(PA/PD)*(BC/YA)*(AX/BC)
Then
when we simplify we get:
(BD/CD)*(XA/GA)*(EC/EA)*(FA/FB)=(AX/GA)
Next
mulitple both sides by (GA/AX)
Then
our final formula is:
(BD/CD)*(EC/EA)*(FA/FB)=1!
We
have proved our conjecture.
What
would happen if P is outside the triangle? You can explore by
using the GSP
Sketch.
Part
III:
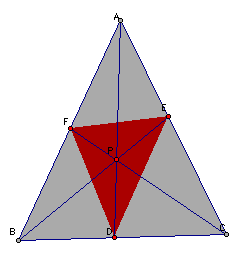
Show that when P is inside the triangle ABC, the ratio of the
areas of the triangle ABC and triangle DEF is always greater than
or equal to 4. When is it equal to 4?
So
we get the ratio: (BD/YA)=(PD/PA)
If
we mulitply the ratios together, we get:
(BD/YA)*(XA/CD)*(EC/EA)*(FA/FB)=(PD/PA)*(PA/PD)*(BC/YA)*(AX/BC)
Then
when we simplify we get:
(BD/CD)*(XA/GA)*(EC/EA)*(FA/FB)=(AX/GA)
Next
mulitple both sides by (GA/AX)
Then
our final formula is:
(BD/CD)*(EC/EA)*(FA/FB)=1!
We
have proved our conjecture.
What
would happen if P is outside the triangle? You can explore by
using the GSP
Sketch.
Part
III:
Show that when P is inside the triangle ABC, the ratio of the
areas of the triangle ABC and triangle DEF is always greater than
or equal to 4. When is it equal to 4?
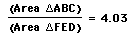 What if
we move point P?
What if
we move point P?
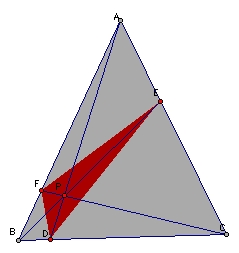
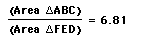 Let's move
point P one more time?
Let's move
point P one more time?
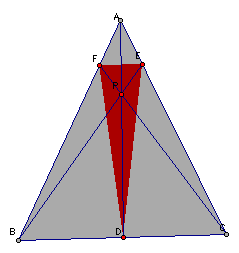
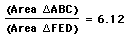 Now let's
explore why our conjecture that the relationship between these
two triangles is greater than or equal to 4.
The medial
triangle DFE is 1/4 of the area of the triangle ABC, so we have
a ratio of 4 to 1.
When does
the ratio equal 4 exactly? Use the link and explore the relationship
when P is on the centriod.
GSP
Sketch
Now let's
explore why our conjecture that the relationship between these
two triangles is greater than or equal to 4.
The medial
triangle DFE is 1/4 of the area of the triangle ABC, so we have
a ratio of 4 to 1.
When does
the ratio equal 4 exactly? Use the link and explore the relationship
when P is on the centriod.
GSP
Sketch
Return