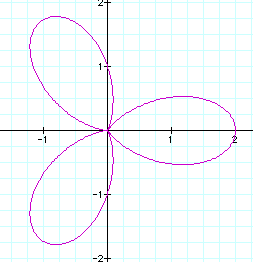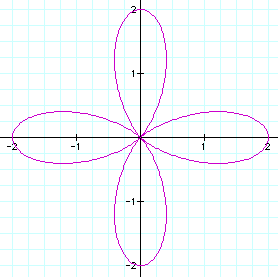Investigation 11
Polar Equations
Charles Meyer
In Investigation 11, I will look at Polar Equations and how
changes within the equation changes the look of the "n-leaf
rose". I will begin by setting up my equation.
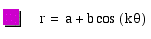
By setting a and b equal to one another and
setting k to an integer, I find the following graphs.
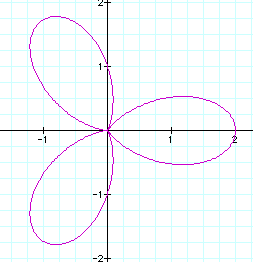
k = 3
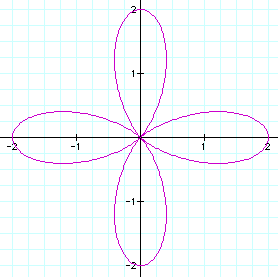
k = 4
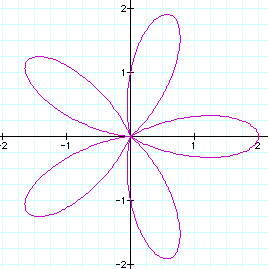
k = 5
Each graph represents something unique about the rose. The
variable k gives the rose the number of leaves it has.
The variables a and b gives the rose its size. However,
when the variable a is removed from the equation, changes
occur within the rose in two areas. One is the size of the rose,
the other is the number of leaves the rose contains.
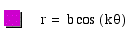
The following examples are of different values of k.
When k is an odd number, the quantity of leaves of the
rose is equal to k, however when k is even, the
number of rose leaves is equal to 2k.
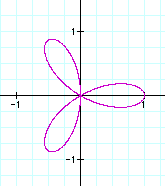
k = 3
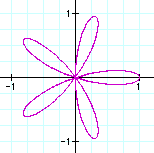
k = 5
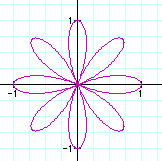
k = 4, number of leaves = 2k = 8
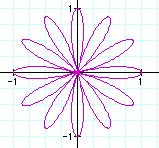
k = 6, number of leaves = 2k = 12
While the cosine function plays a role in the original equation,
it would be interesting to see how its counterpart, the sine function
affects the rose.
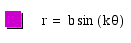
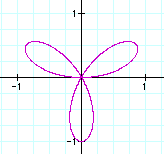
k = 3
At first glance it would appear that no change has occurred
to the rose, but pay attention to the placement of the rose on
the axis. The sine function forces the rose to have a pedal that
is symetric along the y-axis as opposed to the x-axis
of the cosine function.
This investigation would be very beneficial to high school
algebra 3 and trigonometry students. I believe the knowledge of
the changes caused by the variables as well as the changing of
the function would help them understand the power of small changes
to a function.