
Assignment Three
Quadratic Equations
Charles Meyer
For this investigation, I will compare different graphs of
y = x2 + bx + 1. I am concerned about how the graph changes
as values of b change. The values of b that
I really want to concentrate on are b = -3, -2, -1, 0,
1, 2, 3
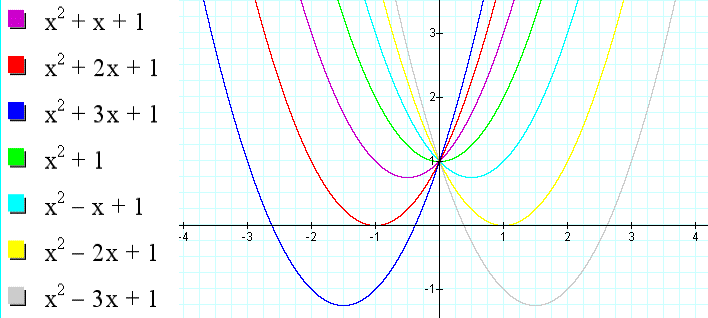
The question is then posed as to what does the changes in
b do to the graph. It is noted that no matter what,
the graphs pass through y = 1 at all values of b.
The graph also helps us to see the roots of each equation.
The graph's intersection with the x-axis, tells the number
of roots and the value of those roots of the equation. If
b < -2 or b > 2 then the equation has two
roots. Those equations when b is less of -2
then both roots are negative, equations where b is greater
than 2, then both roots are positive. Equations where b
is equal to -2 or 2, then the equation has only one root.
Finally b is greater than -2 but less than 2 then there
are no real roots to the equation.
Another interesting part of this graph is the vertices of
each equation. If these vertices are connected, a new parabola,
facing downward is formed.
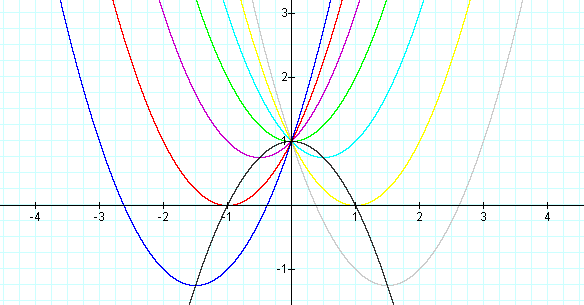
In this investigation, it was discovered that given an equation
of y = ax2 + bx + c, if a and c remain
constant but b varies then the locus of the vertices of
all parabolas will also form a parabola. This investigation
would be very beneficial to a 8th or 9th grade Algebra student
in learning the value of graphing equations.



