Final Assignment
Charles Meyer
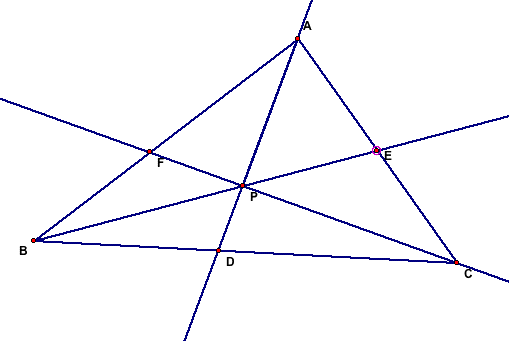
For the final for this class we are asked to create a triangle
ABC with an interior point P.

Next we are asked to extend lines from A to P, B to P, &
C to P. We are then asked to extend those lines so that they intersect
with the line segments of the triangles.
Finally we explore the products of the equations (AF)(BD)(EC)
and (FB)(DC)(EA) for many different triangles.
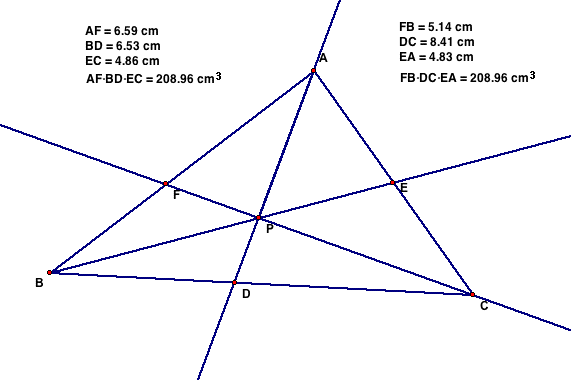
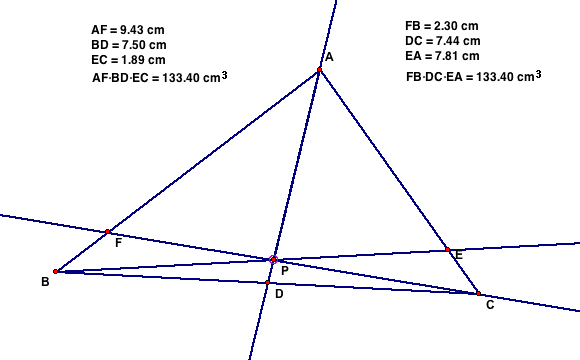
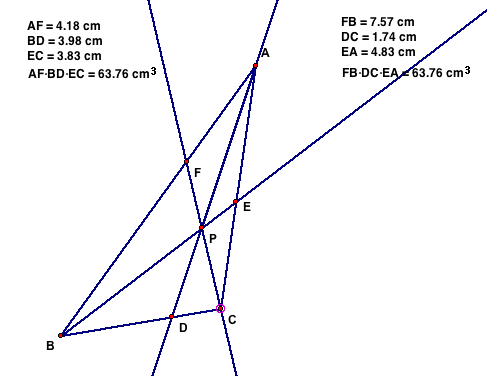
It would appear that no matter what the shape or the location
of the point P, the products of the two equations always are equal
to one another. If a ratio were developed of
(AF)(BD)(EC) /(FB)(DC)(EA), it would always equal 1.00
Now, will it always equal 1, that is the proof I hope to show.
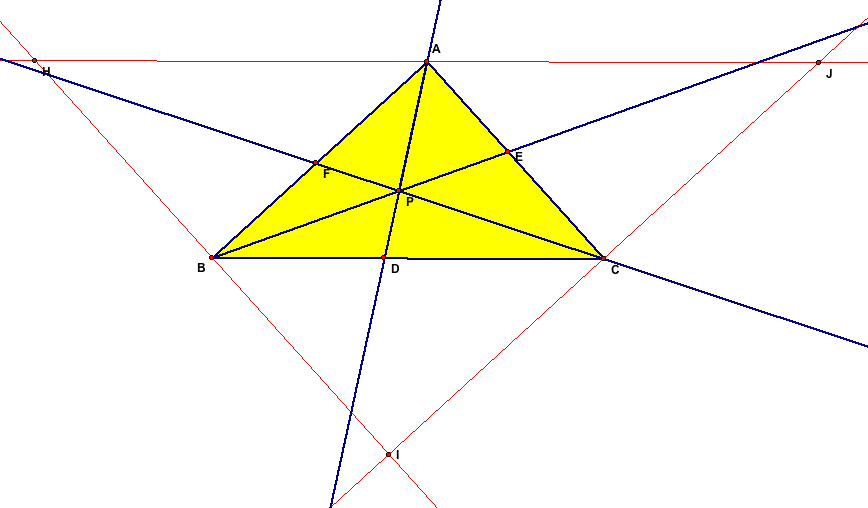
I will begin by creating parallel line segments to those of
my original triangle. If I am correct, the ratio of (JC)(BH)(HA)/(AJ)(IB)(IC)
should also equal 1.
Through calculation, I find that the ratio of the lengths
of the parallel line segments does also give us an answer of 1.
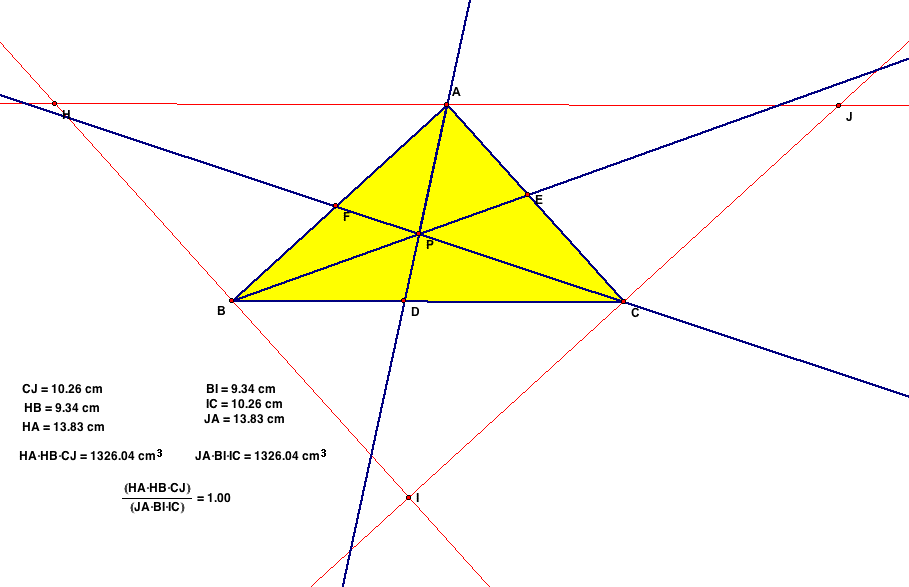
Comparing the original to the expanded triangle, the idea
of similar triangles helps prove that the ratios will always equal
1.
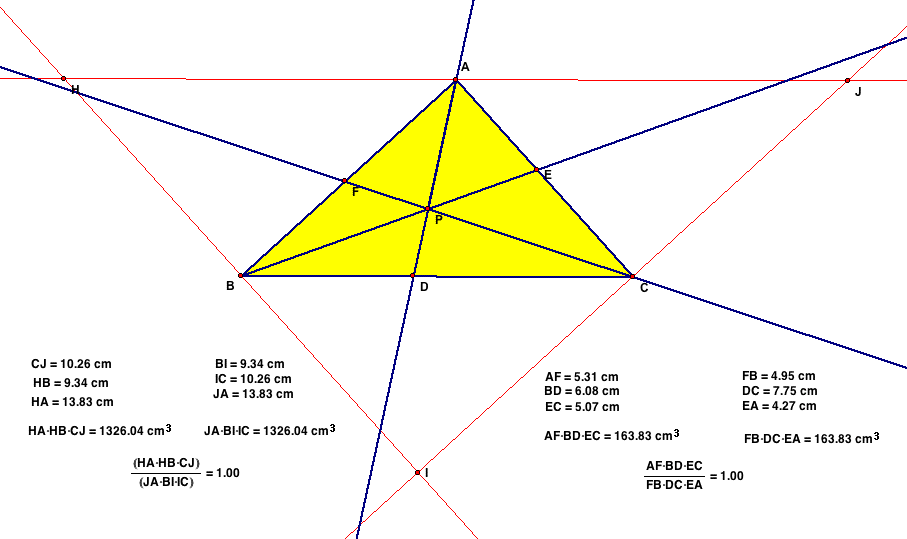
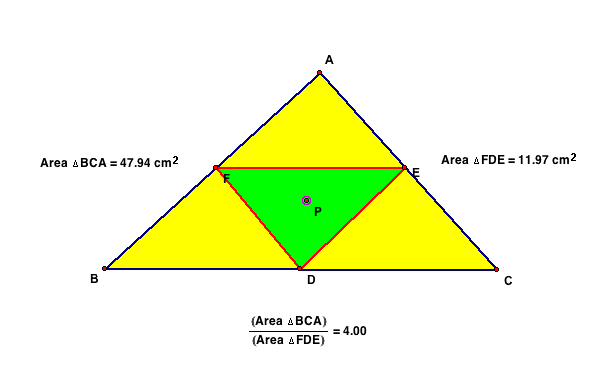
Now we should consider the area of the original triangle ABC
and the new triangle DEF. The triangle is formed when connecting
the points created on the line segments of AC, AB, & BC.
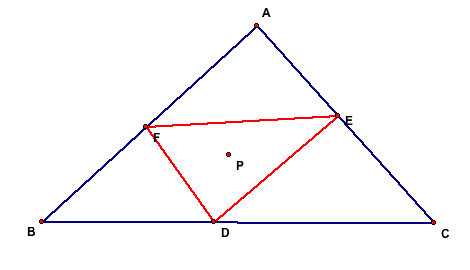
The goal is to find the ratio of the areas of ABC and DEF.
I hope to show that ABC/DEF will always be 4 or greater. Below
are a couple of examples of different triangles ABC & DEF
and the ratios created. Note that value never goes below 4.
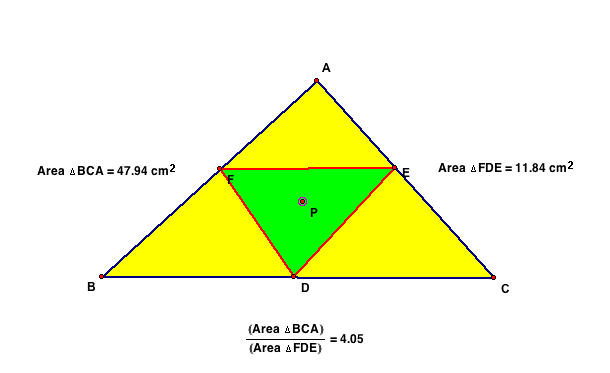
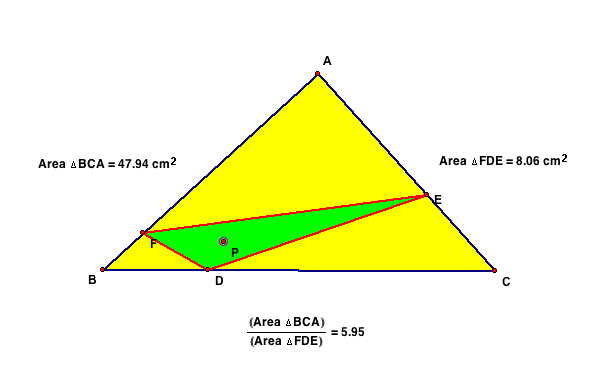
Finally we consider when or if, the value of the ratio will
be equal to 4. The only time that the value will be 4 is when
the segments of the similar triangles are parrallel to each other.
Note that segment EF is parallel to BC, DF to AC, and AB to ED.
An example of this is shown below.