Exploration of the Quadratic Equation

By Brooke Norman

In this assignment, we are going to look at the quadratic equation of:

I will use Graphing Calculator 3.2 to examine the effects of changing the values for ‘a’, ‘b’, and ‘c.’

First, lets explore the equation by letting ‘b’ and ‘c’ equal 1 and varying ‘a’ from -3 to 3. 

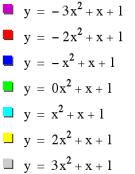
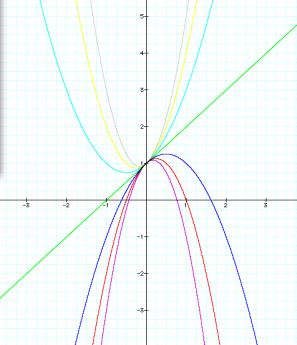
As you can see from the above graphs, each equation crosses the y-axis at 1.  The graph when ‘a’=0 is a straight line that is tangent to the other graphs.  When ‘a’ is a positive number, the parabolas are concave up and when ‘a’ is negative, the parabolas are concave down. As ‘a’ changes, so do the vertexes. As the value of ‘a’ increases, the parabolas become more steep and skinnier.   

Now, lets explore the equation but this time lets let ‘a’ and ‘c’ equal to 1 and let ‘b’ vary from -3 to 3.

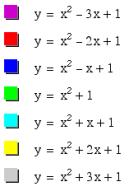
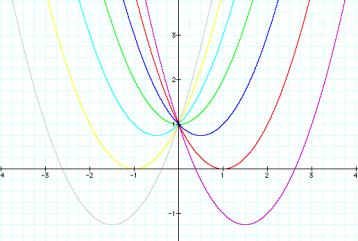
The graph shifts to the left as ‘b’ increases in a positive direction and the graph shifts to the right as ‘b’ increases in a negative direction. Notice that the vertex shifts as ‘b’ is varied.

We are now going to explore the equation but this time lets let ‘a’ and ‘b’ equal to 1 and let ‘c’ vary from -3 to 3.

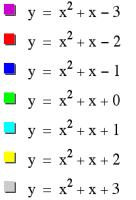
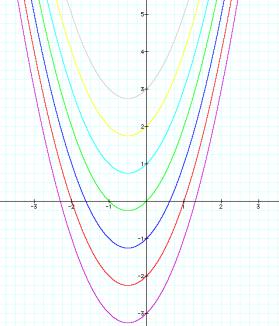
As you see, when ‘c’ varies, the vertex is shifting up and down. Therefore ‘c’ is changing the y-coordinate of the vertex.

In conclusion:

The position of the vertex is affected by ‘a, b, and c.’ The x- and y-coordinates of the vertex are affected by ‘a and b’ and only the y-coordinate appears to be affected by ‘c.’ It also appears that ‘a’ also determines the steepness and he direction of concavity of the parabola.

Return to Brooke’s EMAT 6680 Homepage.