Graphical Exploration!

By

Brooke Norman

Have you ever thought about what changing the exponents in an equation really does to its graph?

I am going to look at a simple function of xⁿ+yⁿ=1, change its exponents, look at the patterns of the graphs and see if I can predict what the graph of a larger exponent will look like.

We will first begin by graphing the following functions:

 

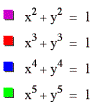
Lets explore these graphs closer:

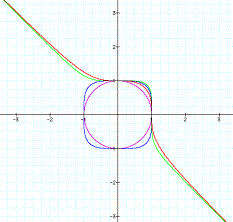
We will begin with the even exponents:

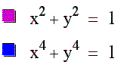
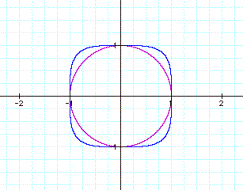
From the graph above, you can see that the larger the even number gets, the more “squared off” the corners become. The smaller the even exponent, the more “rounded off” the corners appear. This leads me to believe that an exponent of 24 will be more of a perfect square with 90° corners, than a circle. Let’s graph it and see if we are right.

 

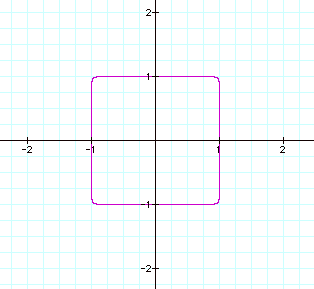
We will now look at the odd exponents:

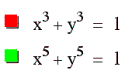
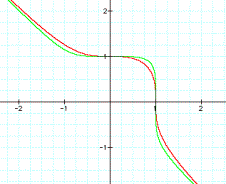
We can see that as the odd exponent gets larger, the “hump” of the graph begins to become more squared. The smaller the odd exponent, the more rounded the “hump” of the graph appears. This leads me to believe that an exponent of 25 would be very squared off. Lets see if my prediction is correct.

 

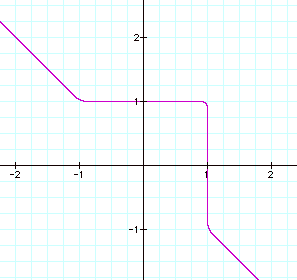
In conclusion:

By increasing the exponent in the equation of xⁿ+yⁿ=1, the corners of the graphs become more defined or sharper. By decreasing the exponent in the equation of xⁿ+yⁿ=1, the edges become more rounded and softer.

 

Return to Brooke’s EMAT 6680 Homepage.