
Tangent Circles
By: Brooke Norman
Given two circles and a point on one of the circles, construct a circle tangent to the two circles with one point of tangency being the designated point.
Start out with a large circle of any size, label the center A. Then construct a smaller circle inside this large circle, label the center B.
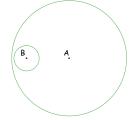
Next place an arbitrary point on each circle and label them C and D.
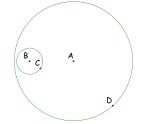
Construct a line segment from B to C. This will be used for the radius of a
circle with center D. Also, create
a line that goes through points A and D.
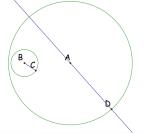
Now, we are going to use line segment BC to create a like circle
with center, D.
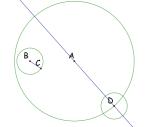
We will now label a point, E, that lies on the new circle and also
on the new line.
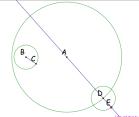
We will now draw a line
from point B to point E and label its midpoint.
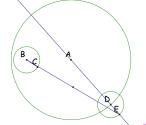
Next we will draw a line perpendicular to line BE and going
through the midpoint F.
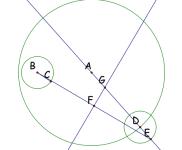
The last step is to create a circle
with a radius the length of GD.
This creates our circle that is tangent to two other circles.
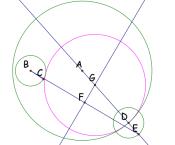
If we hide all of our tools for construction, we should be left
with a picture that looks like:
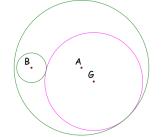
If you would
like to play around with tangent lines, use the following link to go to a
script tool for tangent circles.
Return to EMAT 6680 Class
Page for Brooke Norman.