Altitudes and Orthocenters

By

Brooke Norman

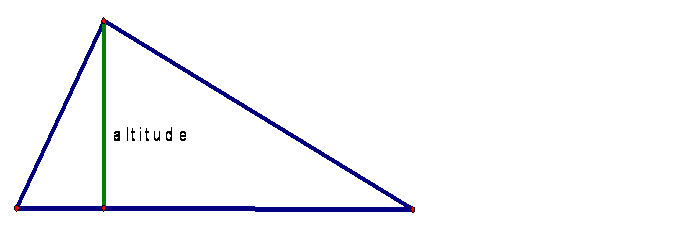
The altitude is also known as the height of a triangle. It is a line perpendicular to a side of the triangle that goes through the opposite vertex of a triangle.

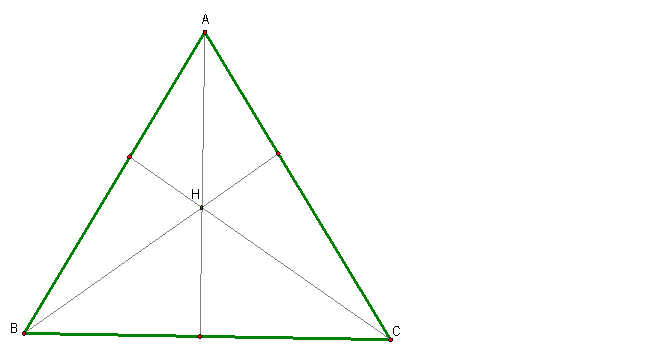
There are three altitudes in every triangle. The intersection of these three is called the orthocenter. It is usually labeled, H.

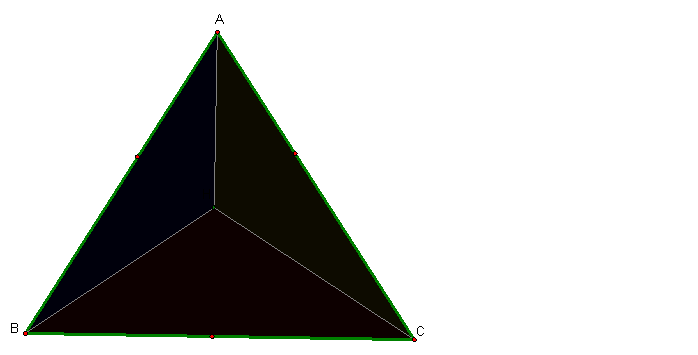
As you can see, the triangle is now broken up into three smaller triangles. The are triangles AHB, AHC, and BHC.

We will now find the orthocenters of each of these triangles.

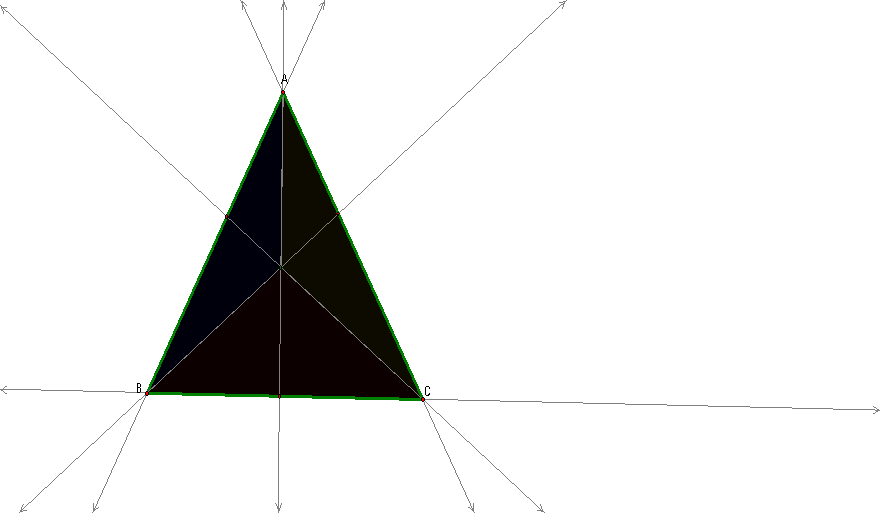
As you notice, the orthocenters of the three inner triangles lie on the vertices of the original triangle.

The orthocenter of triangle AHB is C

AHC is B

BHC is A

We will not construct the circumcircles of all four triangles. It should look like this:

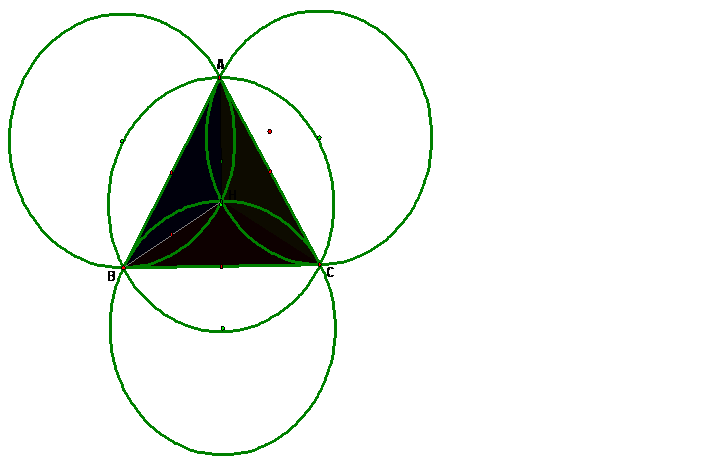
If you connect the origins of the three circumcircles to their nearest vertices of the original triangle ABC and to the orthocenter, H, you form a cube!

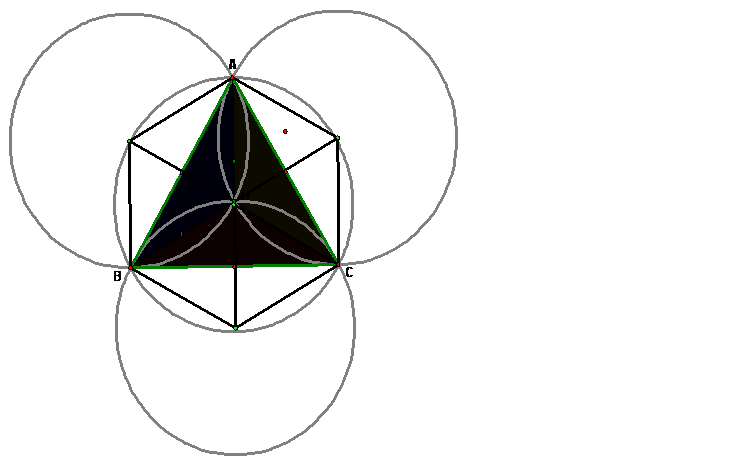
You may play around with this construction by clicking here. Try moving the different points around and see what happens.

Here are some interesting things to take note of:

Each of the four circumcircles have the same radius.

The orthocenters of the three inner triangles in the original triangle lie on the vertices of the original triangle.

The lines going from the orthocenter H of the original triangle from the center of each circumcircle, and the two closest vertices of the original triangle, form a cube.

The lines used to construct the orthocenter of the original triangle ABC bisect the overlapping areas of the outer circumcircles.

Return to Brooke’s EMAT 6680 Homepage.