Pedal Triangles

By

Brooke Norman

What is a pedal triangle?

We will first construct a triangle and pick any arbitrary point, P, in the plane.

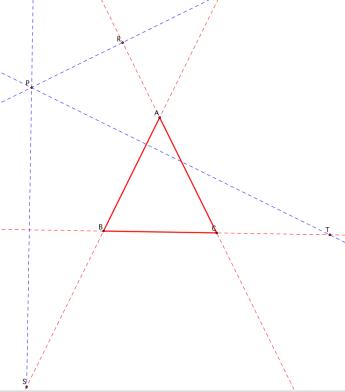
The next step is to mark the intersections of the perpendicular lines to each side of ABC from point P. The lines may need to be extended in order to see their intersections, labeled R, S, T.

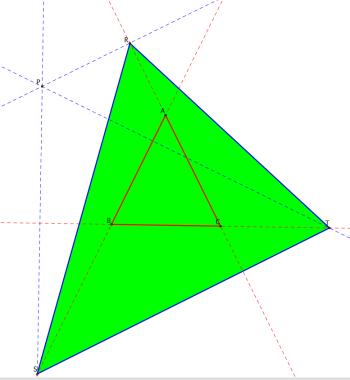
We will now connect the points RST to form the pedal triangle for point P.

To form your own pedal triangle from any point, you may use this script tool.

Now lets see what happens when we place P in different places:

-P is at the centroid…

Remember, the centroid is the common intersection of the medians.

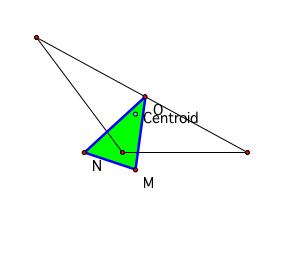
As you can see, the vertices of the pedal triangle lie on the sides of the original triangle.

-P is at the incenter…

Remember, the incenter is the point on the interior of the triangle that is equidistance from all three sides.

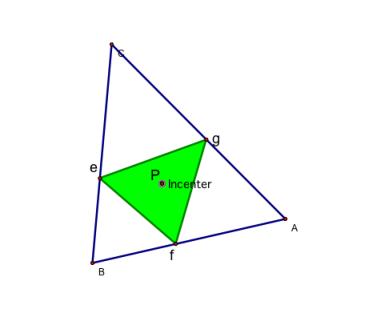
Just as with the centroid, the vertices of the pedal triangle when P is the incenter will always lie on the sides of the original triangle.

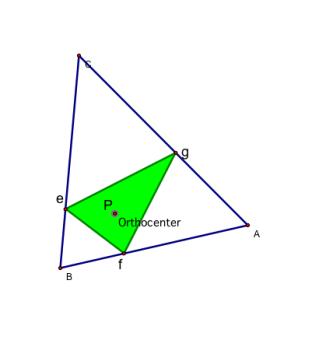
-P is at the orthocenter…

Remember that the orthocenter is the common intersection of the three lines containing the altitudes.

This is with the orthocenter inside ABC.

This is with the orthocenter outside of ABC.

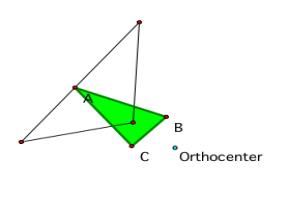
As you can see, it appears that as long as the orthocenter remains inside of the triangle, the pedal triangle remains similar to the previous two cases. Take notice that no matter where P is located, the vertices of the pedal triangle remain on the altitudes of the original triangle.

-P is at the circumcenter…

Remember that the circumcenter is the point in the plane equidistance from the three vertices of the triangle.

When the circumcenter is inside ABC.

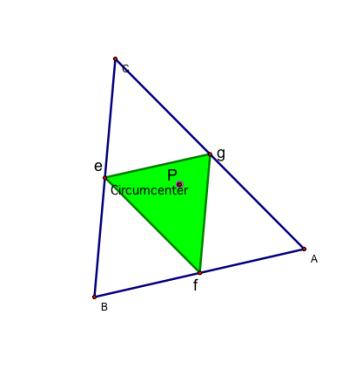
When the circumcenter is outside of ABC:

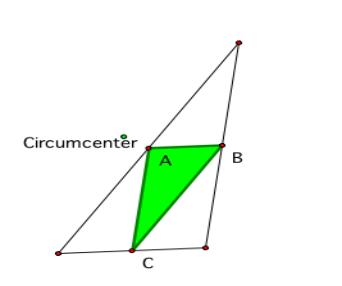
The case of the circumcenter is similar to the orthocenter. However, in this case, the vertices of the pedal triangle always lie on the perpendicular bisectors of the original triangle.

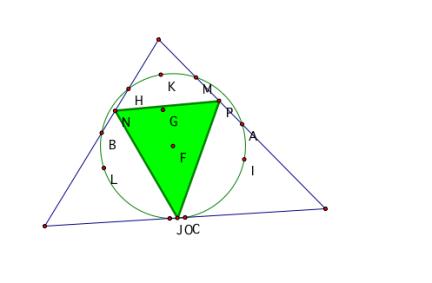
-P is the center of the nine point circle for triangle ABC…

-P is on a side of ABC…

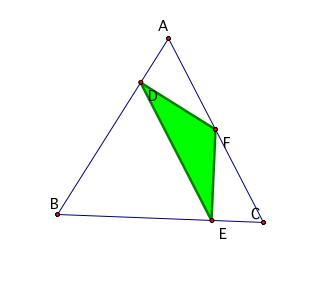
Take notice that P lies on one of the vertices. Which ever side P is on, the vertex for that side is the same.

-P is one of the vertices of ABC…

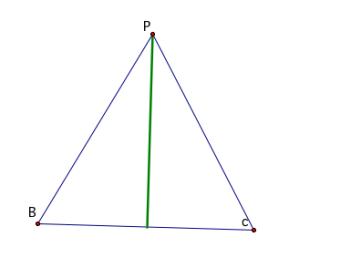
It appears that there is no pedal triangle for this case. This is a special case and a degenerate triangle has been formed. The three vertices of the pedal triangle are collinear. The green line segment above is called the Simson line.

Are there any other conditions in which the three vertices of the pedal triangle are collinear, or a degenerate triangle is formed? How about when P lies on the circumcircle. Click here to see what happens.

As you can see, anytime P lies on the circumcircle, the simson line is formed.

Return to Brooke’s EMAT 6680 Homepage.