
By Brooke Norman
Iterations of Sine and Cosine
What is iteration?
Iteration is the process or action of repeating an application.
In this essay, we will look at the iterations of the graphs
of sine and cosine.
Below is the graph of y=sin(x).
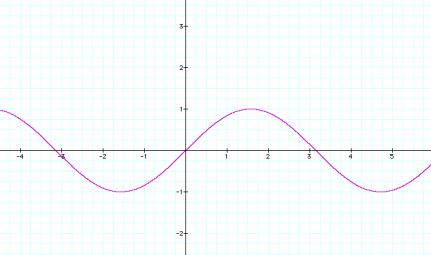
Here it has been iterated seven times. So, it looks like:
Purple: Y=sin(x),
Red: Y=sin(sin(x),
Blue: Y=sin(sin(sin(x))),
Green: Y= sin(sin(sin(sin(x)))),
Lt. Blue:
Y=sin(sin(sin(sin(sin(x))))),
Yellow:
Y=sin(sin(sin(sin(sin(sin(x)))))),
Gray:
Y=sin(sin(sin(sin(sin(sin(sin(x)))))))
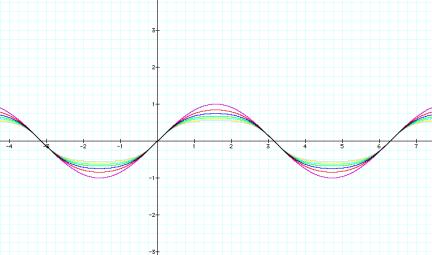
As you notice, the graph of the sine curve is progressively
flattening out. One may
hypothesize that the curve is approaching zero. Without the help of technology,
this would take hours and hours of work to see. We can iterate the sine curve hundreds of times in order to
see that it is approaching zero, in a matter of minutes to see this
pattern.
What about cosine?
Here is the graph of y=cos(x).
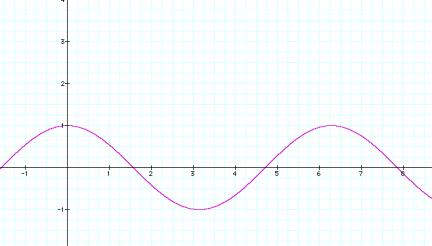
LetŐs iterate it six times also. We will get the following:
Y= cos(x),
Y=cos(cos(x)),
Y=cos(cos(cos(x))),
Y=cos(cos(cos(cos(x)))),
Y=cos(cos(cos(cos(cos(x))))),
Y=cos(cos(cos(cos(cos(cos(x)))))),
Y=cos(cos(cos(cos(cos(cos(cos(x))))))).
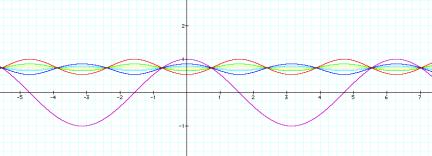
As you can see, the cosine curve appears to be approaching
one. LetŐs see if we can
figure out what the exact value is.
Here cosine is iterated 12 times.
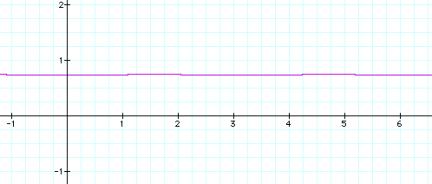
From this graph, it looks like the number is between .7 and
.75. Also notice that it took a
lot less iterations to find the limit of the cosine function.