Final Assignment

By

Brooke Norman

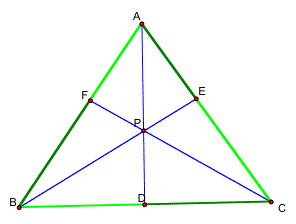
We will first consider any triangle ABC. Then we will select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

Now lets explore (AF) (BD) (EC) and (FB) (DC) (EA) for various triangles and various locations of P.

Click here to manipulate a GSP sketch for different locations of P.

Did you notice that as you moved P, (AF) (BD) (EC) = (FB) (DC) EA)?

Why does this happen? Lets prove it!

First we will construct parallel lines to produce similar triangles. Line HG is parallel to segment BC.

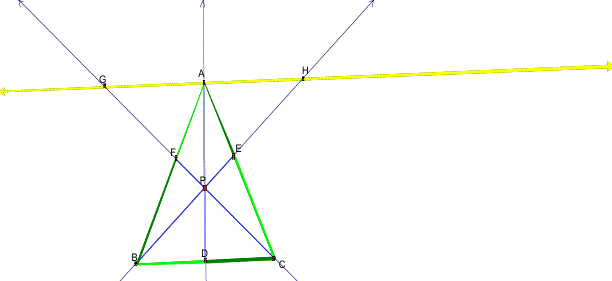
You may notice that there appears to be several similar triangles. Lets compare two, AEH and CEB.

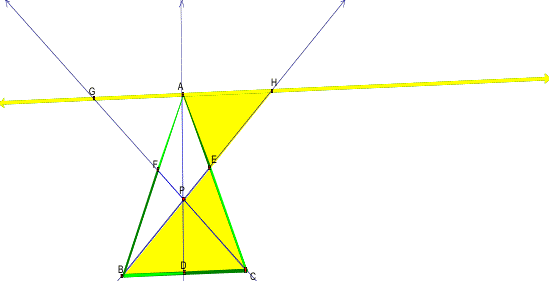
You can see that EH/EB = AE/EC = AH/BC. This proves that Triangle AHE is similar to CEB.

You can also prove other triangles are similar, such as Triangles FAG and FBC, and Triangles AHP and DBP.

After looking at all the segments, we find that:

AE/EC=AH/BC

BF/FA=CB/AG

AG/CD=AP/PD

AH/DB=AP/DP

From AH/CD=AP/PD and AG/DB=AP/DP you get AH/CD=AG/DB

Therefore you now know CD/DB=AH/AG

by multiplying the first, second and last equations, we get:
(AE/EC)(BF/FA)(CD/DB) = (AH/CB)(CB/AG)(AG/AH) = (AH)(CB)(AG)/(CB)(AG)(AH) = 1

This proves that the ratio of the sides equals 1.

Does this proof hold true even when P is outside of the triangle? Click here to explore it on your own.

When P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF are always greater than or equal to 4. When does it equal to 4?

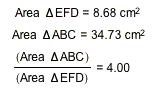
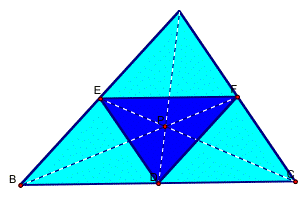
The ratio equals exactly 4 when P is located at the centroid of the triangle.

This concludes my exploration of the final assignment. Hope you enjoyed it.

Return to Brooke's EMAT 6680 Homepage.