
Modular Arithmetic is a form of arithmetic dealing with the remainders after integers are divided by a fixed "modulus" m. Basically, it is a kind of integer arithmetic that reduces all numbers to ones that belongs to a fixed set [0 ... N-1]. We can say two integers, a and b, are congruent mod m (where m is a natural number) if both numbers divided by m produce the same remainder. In other words, m must evenly divide their difference, a - b. We write:

For example, let's look at arithmetic in mod 6. In this case, our fixed modulus is 6, so we say "mod 6." Here, operations of addition and multiplication with integers will result in a number that is divisible by 6 with a remainder of either 0, 1, 2, 3, 4, or 5.
We can see that two different numbers can be represented as congruent in mod 6. Notice above that both 10 and 28 are congruent to 4 in mod 6.
So, we can use Microsoft Excel to generate tables to describe addition and multiplication in mod 6. Notice how the only numbers to appear in the tables below are 0, 1, 2, 3, 4, and 5. Any natural number, when divided by 6, will produce one of these 6 remainders.
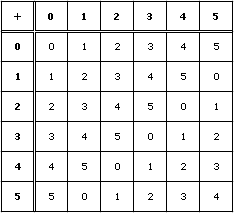
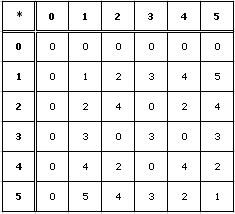
Notice from the table 5 + 5 = 4. This seems strange in the usual sense of addition we are used to, but notice that in mod 6 this is true. In fact, 5 + 5 = 10, and we know that 10 is congruent to 4 (mod 6). So, it is true 5 + 5 does actually equal 4! Similarly the table above tells us 5 * 5 = 1. Now this no longer comes as a surprise because we know 5 * 5 = 25, but 25 is actually congruent to 1 (mod 6). Therefore, 5 * 5 = 1! The tables above are accurate for addition and multiplication... in mod 6 of course!
We have already seen that one way to generate an entry in Pascal's triangle is to add the two numbers above, in the preceding row. So all of the entries in Pascal's Triangle are the sum of two other entries. When the entries of Pascal's Triangle are expressed in terms of modular arithmetic we notice some really interesting patterns. The investigations of this essay will explore the patterns of Pascal's triangle using mod p, where p has been chosen to be a prime number 2, 3, 5, and 7.
For more on Modular Arithmetic, please visit
MathWorld.
Return to Essay 1: Pascal's Triangle and Modular
Exploration