Area and Perimeter of Regular Polygons

Pentagon

Content Objective:

Students will learn the method of finding the perimeter of regular pentagons.

Students will discover two methods for finding the area of regular pentagons.

Materials:

Rulers for pairs, pentagon perimeter worksheet, pentagon area worksheet

Procedure:

Perimeter

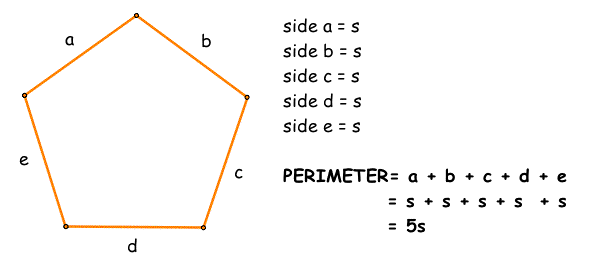
1. Collectively recall the definition of perimeter given on review day. Have students get into pairs and distribute perimeter worksheet. Once worksheet is complete and students have compared their answers, ask the class as a whole the following questions:

What do you notice about the side lengths of our pentagon?

What happens to the perimeter when the side lengths are changed?

Is there a way to find the perimeter of a regular pentagon without measuring all five sides?

Recalling the general expressions for the perimeter of regular triangles and squares. Do you notice a pattern? What can we expect when we discover the perimeter of an octagon?

2. Demonstrate using Geometer's Sketchpad the properties of the side lengths of regular pentagons. Click here to use the GSP file and watch the animation for the changing perimeter.

Area

Similar to the hexagon, first we will divide the regular octagon into parts to find the area. Then, we will identify and use the apothem to find the area of our regular pentagon and compare both of the methods.

METHOD 1:

Begin by showing the figures below and ask the following questions:

Click here to view the GSP sketch of these images.

First, how can we break this figure into familiar shapes?

Are these triangles regular? How can you tell?

Since these triangles are not regular, how would we find the area of ONE of them?

What is a quick way to find the area for the entire pentagon?

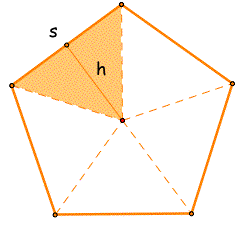
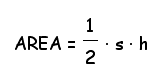
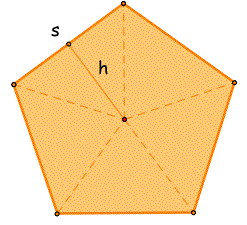
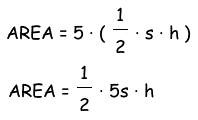
So we have discovered a general formula for the area, using the smaller triangles inside the pentagon!

Example 1:

Use the area expression above to calculate the area of a pentagon with side length of s = 4.00cm and a height of h = 2.75cm for comparison with method 2 later.

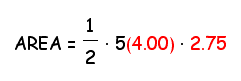
METHOD 2:

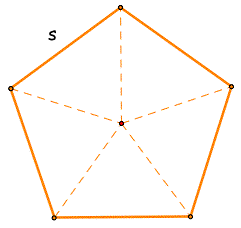
Recall the formula for area using the apothem found for regular hexagons.

 

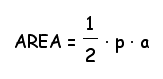
Discuss the concept of apothem with students and ask the following questions:

How does this formula relate to regular pentagons? What is the perimeter p of a regular pentagon?

What does the apothem of a regular pentagon look like?

How is the apothem related to the height we found in the regular pentagons above?

How many apothems does a regular pentagon have? Are the apothems all the same length?

Let's make sure by using this expression to find the area from Example 1.

Example 2:

Now we can fill in the values for p and a to find the area of this regular hexagon. Again, let s = 4.00cm and let a = 2.75cm. What is the area?

COMPARING METHODS:

Discuss with students the two different methods for finding the area of a regular pentagon.

As a class, discuss the advantages and disadvantages for each of the methods and ask the following questions:

Which method is easier to formulate?

Will these methods ever produce different answers?

So we can see the general formula using the apothem we found in regular hexagons applies to regular pentagons as well. Since it is a general formula, will it be useful for any of our polygons?

What values of our polygon do we need to know to use this formula?

Finally, distribute the pentagon area worksheet and have students complete in groups, using either method. Then, as a class, compare answers and discuss the methods for finding the solutions.

Demonstrate using Geometer's Sketchpad the properties of the side lengths and apothem lengths of regular pentagons. Click here to use the GSP file and watch the animation for the changing area.

Return to Instructional Unit