What would happen to our graphs if we replace cos (k theta) from our original equation with sin (k theta) to form a new equation. Let's investigate different values of a, b, and k with this new equation:
To investigate different values of a, let b=1 and k=1. Let's see what happens to our graph when a changes.
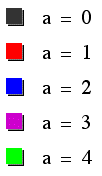 |
 |
Clearly, this equation generates similar graphs
as seen by our original equation containing cos (k theta). The
difference here, however, seems to be that our graphs have rotated
90 degrees counter-wise about the origin, and are now symmetrical
about the y-axis.
To investigate different values of b, let a=1 and k=1. Let's see what happens to our graph when b changes.
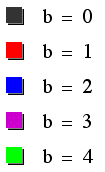 |
 |
This new equation generates similar graphs
for varying values of b as well. Compare these with our original
graphs for the equation containing cos (k theta). The difference
here also seems to be that our graphs have rotated 90 degrees
counter-wise about the origin, and are now symmetrical about the
y-axis.
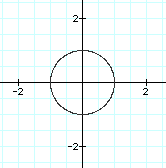
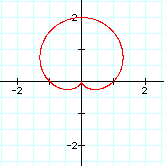
To investigate different values of k, let a=1 and b=1. Let's see what happens to our graph when k changes. It is easier to view the effect of a changing k value if these graphs are viewed individually.
|
|
|
|
|
|
 |
 |
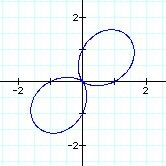 |
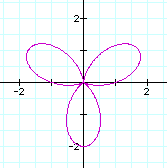 |
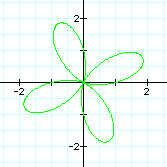 |
These graphs generated by our new equation are similar to those generated by the equation containing cos (k theta). For example, the number of pedals in our "n-leaf rose" is still the value of k. The difference here however, concerns the orientations of the graphs. When k=1 for example, this graph is rotated 90 degrees clock-wise about the origin. Notice when k=2 that the graph is not simply rotated 90 degrees. Similarly with the graph when k=3 and k=4. Do you notice a pattern? View the animation of both the original and new equations below to see the difference in the orientation of these graphs.
View the animation as the value of k goes from 0 to 25 and watch as more "pedals" are generated with this new equation containing sin (k theta).
Watch what happens when the values of a, b, and k all change together from 0 to 10. See how the "n-leaf rose" is generated this way.
How does this compare to our original equation containing cos (k theta)? Watch the animation as both of our equations are graphed with their k values going from 0 to 25.