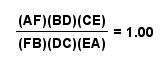
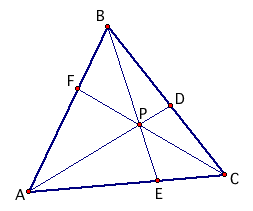
Consider the triangle we have been investigating:
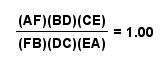
When point P is moved outside of the triangle, (AF)(BD)(CE) and (FB)(DC)(EA) are not defined. Click here to change the location of point P to outside of the triangle. Notice what happens to the corresponding calculations.
If we construct the triangle with lines, instead of segments, we can safely move point P outside of the triangle and maintain the relationship of segment ratios that we have already discovered.
First, construct triangle ABC using lines.
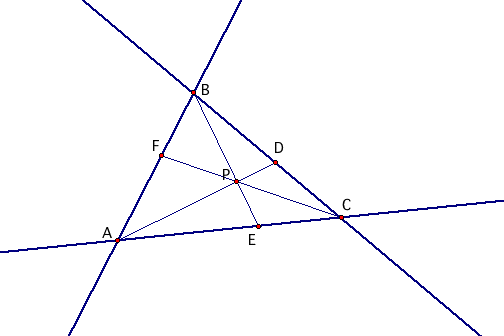
So, what happens if we move point P outside?
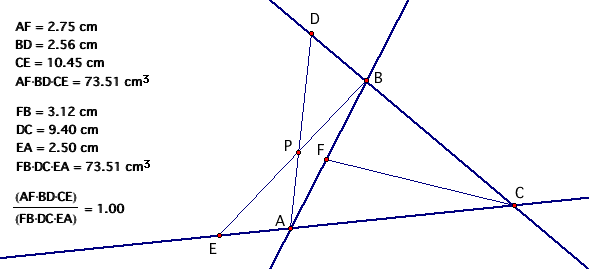
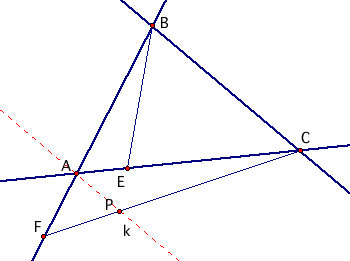
By moving point P outside the triangle, we can see that our ratio of segments is still defined, and is still equal to 1.00. Notice points E and D stay on lines AC and BC respectively. Click here to move P around the outside of triangle ABC. When is the ratio of segments defined? When is the ratio of segments undefined?
As we explore different locations for point P outside of the triangle, we notice that there are certain locations when (AF)(BD)(CE) and (FB)(DC)(EA) are not defined. For example, when P is moved to:
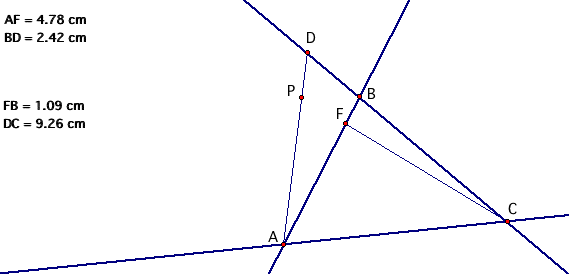
Notice here that point E has disappeared completely. Recall that point E was being traced along line AC. It seems as though when point P is on a line parallel to AC at point B, point E is no longer defined. Remember that E was connecting B with the line AC, through P. Well, when P is moved on a line parallel to line AC, B can no longer be connected to line AC. Parallel lines will never touch, and therefore E is not defined. Without E, our ratio of segments is undefined.
 |
 |
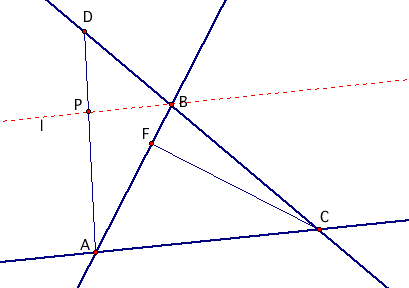In fact, this is true for whenever point P lines on a line that passes through any vertex of triangle ABC, and is parallel to the opposite side. Notice below how points F and D are undefined.
 |
 |
 |
 |
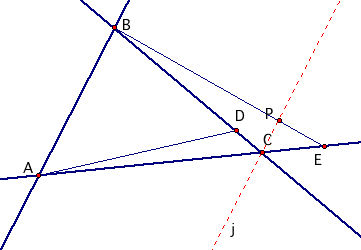There are also several other points of P where
D, E, or F are undefined as well. The parallel lines shown above
play an important role in determining the location of P, so that
there is a point D, E, and F. With these points, our ratio of
segments is defined, an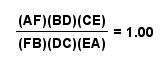d . Whenever
P lies outside these parallel lines (line j, line k, and line
l), the ratio is undefined. So, in order for our ratio to hold
true, point P must line inside the larger triangle
created by the intersection of these parallel lines! As shown
below, P must lie within the light blue triangle for (AF)(BD)(CE)
and (FB)(DC)(EA) to be defined!
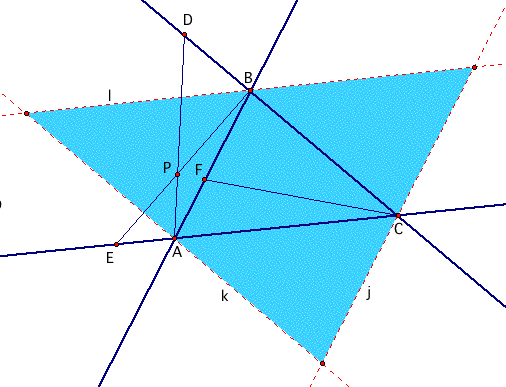
Explore different points of P outside these parallel lines to see that our ratio is no longer defined.