

This assignment is an investigation of polar equations of the form below.
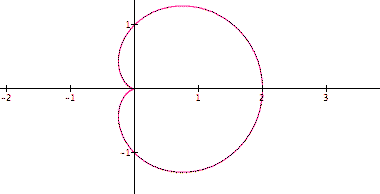
In the example above, a = 1, b = 1, k=1, and theta goes from 0 to 2pi.
In the example below b, the coefficient of cos, is increased to 2, while a and k are held at 1. This creates an inner loop in the graph that extends to 1 unit on the x-axis and the outer loop moves from 2 to 3 units on the x-axis.
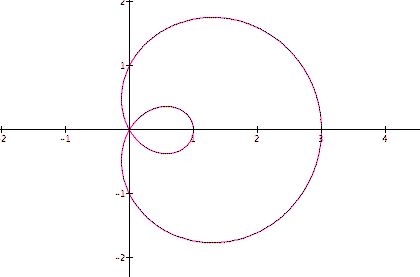
When b is increased to 3, the inner and outer loops both increase by 1 unit on the x-axis.
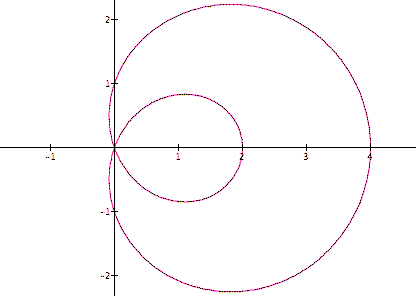
Now with b and k at 1 unit and a increased to 2 we get the following graph. The inner loop in no longer in the graph and the graph seems to be headed toward becoming more circular.
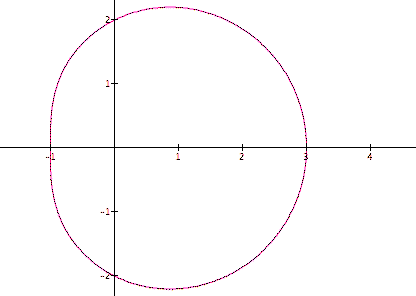
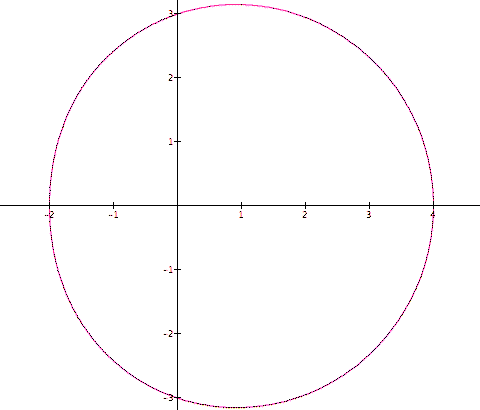
The graph below, with a=3 and b and k=1, seems to be a circle centered at (1,0).
When a and b are 1 and k is increased to 2 we get the following.
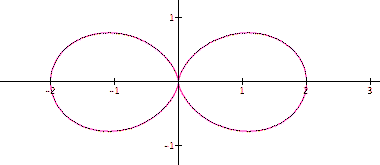
When k is increased to three we get the following graph. The graph has three loops. Changing k, the coefficient of theta, changes the number of loops in the graph.
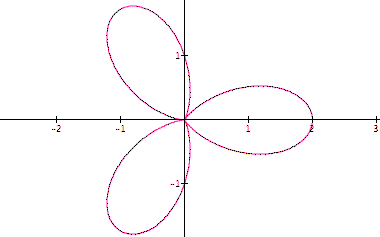
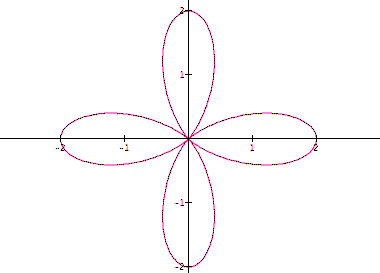
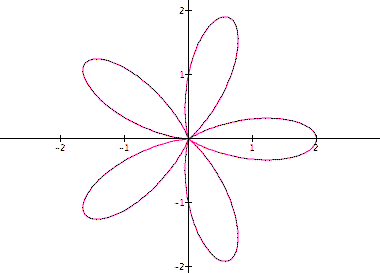
These graphs confirm that when a and b are equal and k is an integer n we get one text book version of the "n-leaf rose." Lets compare this results with the following graph.
In the graph above b and k are both 1 the graph is a circle.
From the 5 graphs above we can determine that when k is odd the graph has k loops, and when k is even the graph has 2k loops.
The length of the "leaf" is determined by b. It is b units in length.
Now lets replace cos() with sin().
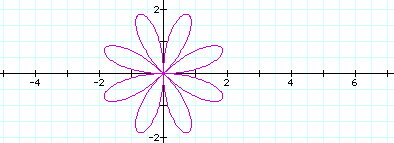
In these instances the graphs are rotated about the origin.
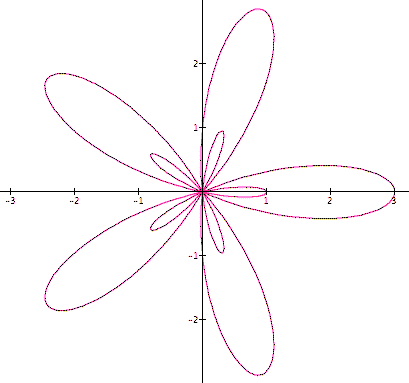
When a and b are not equal in the graph above, k inner loops of length a appear.
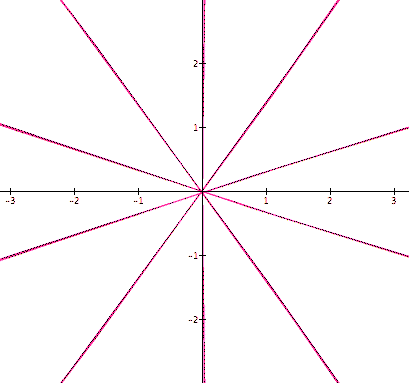
When b is increased to 100 the loops turn into straight lines.
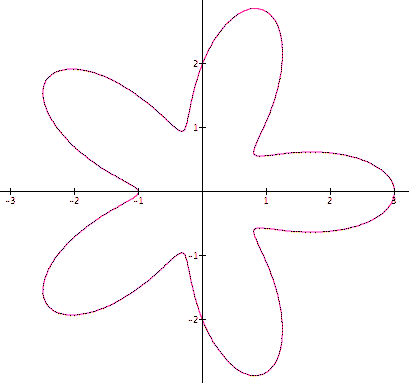
Increasing a causes an opening of the center.