

In this assignment we explore the Pedal Triangle. Let triangle ABC be any triangle. Then if P is any point in the plane of triangle ABC, then the triangle formed by constructing perpendiculars to the sides of ABC and connecting the points of intersection is the Pedal Triangle for Pedal Point P.
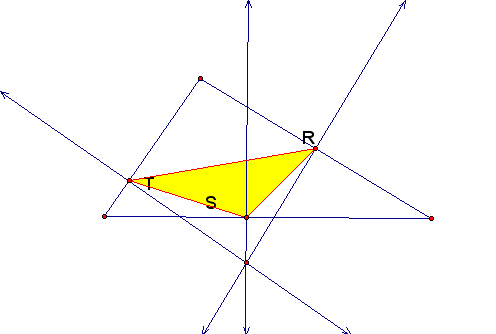
Triangle RST is the Pedal Triangle for Pedal Point P in the figure below. The Pedal triangle was formed be constructing perpendicular lines from the point P to the sides of triangle ABC.
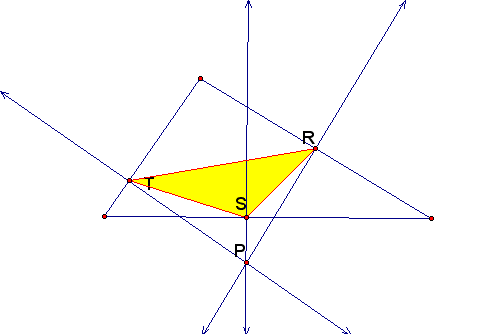
Click here to see and investigate the pedal triangle when the three perpendicular lines intersect the sides of the host triangle.
Click here to see and investigate the pedal triangle at the triangle centers of the reference triangle. Be sure to place the Pedal Point over each triangle center point.
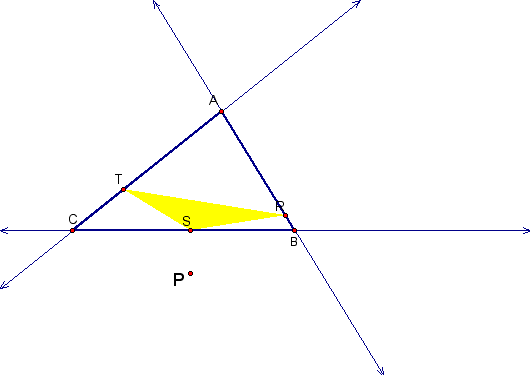
Click here to see and investigate the pedal triangle when the Pedal Point P is any point in the plane of triangle ABC.
This is an example with the Pedal Triangle outside the host triangle.