

_____________________________________________________________________________________________
_____________________________________________________________________________________________
On a dark night, we can often see a band of light stretching across the sky. This band is the Milky Way galaxy -- a gigantic collection of stars, gas and dust. Far beyond the Milky Way, there are billions of other galaxies -- some similar to our own and some very different -- scattered throughout space to the very limits of the observable universe.
Types of Galaxies
Astronomers classify galaxies into three major categories. Spiral galaxies look like flat disks with bulges in their centers and beautiful spiral arms. Elliptical galaxies are redder, more rounded, and often longer in one direction than in the other, like a football. Galaxies that appear neither disk-like nor rounded are classified as irregular galaxies.
Spiral galaxies usually consist of three components: a flat disk, an ellipsoidal bulge and a halo. The disk contains a lot of interstellar gas and dust, and most of the stars in the galaxy. The gas, dust and stars in the disk rotate in the same direction around the galactic center at hundreds of kilometers per second and are often arranged in striking spiral patterns. The bulge is located at the Centrex of the disk and consists of an older stellar population with little interstellar matter. The near-spherical halo surrounds the disk, and is thought to contain copious amounts of dark matter : matter that acts gravitationally like "normal" matter but that can't be seen! Astronomers infer the presence of this dark matter by the motions of stars and gas in the disk of the galaxy, as well as older stellar populations in the halo like globular clusters. The young stars in the disk are classified as stellar population I, and the old bulge and halo stars as population II.
Astronomers classify spiral galaxies according to their appearance by using the Hubble scheme. Those with pronounced bar structures in their centers are called "barred spirals" and are classified "SB" (examples are given in brackets). Galaxies with conspicuous bulges and tightly wound spiral arms are called "Sa" ( Sombrero galaxy ) or "SBa" ( NGC 3185 ). Galaxies with prominent bulges and pronounced spiral arms are classified as "Sb" ( M31 , M81 ) or "SBb" ( M95 , NGC 4725 ). Other spirals with loose spiral arms and a small bulge are classified as "Sc" ( M33 , M74 , M100 ) or "SBc" ( M83 , M109 ), (Curious About Astronomy? Ask an Astronomer) .

(via Astronomy Picture of the Day ) M51: The Whirlpool Galaxy. The Whirlpool Galaxy is a classic Sc type spiral galaxy visible with binoculars in the constellation of Canes Venatici. It is 23 million light years distant and is one of the brightest and most picturesque galaxies on the sky. The smaller galaxy appearing below and to the left is behind M51 and is thought to be responsible for the spiral structure of M51.



To see a GSP sketch showing the measurements approximating the spirals click below.
M51 has two (Fibonacci number) spirals in one direction. To see a GSP sketch showing the measurements approximating the spirals, click below.
Click 
Logarithmic Spirals Isabel and M51
Credit: Comparison and M51 image copyright Brian Lula ; Hurricane Isabel, courtesy GHCC, NASAExplanation: Uncomfortably close hurricane Isabel (left) and 30 million light-year distant galaxy M51 actually don't have much in common. For starters, Isabel was hundreds of miles across, while M51 (the Whirlpool Galaxy ) spans about 50,000 light-years making them vastly dissimilar in scale, not to mention the extremely different physical interactions which control their formation and evolution . But they do look amazingly alike, both exhibiting the shape of a simple and beautiful mathematical curve known as a logarithmic spiral , a spiral whose separation grows in a geometric way with increasing distance from the center. Also known as the equiangular spiral , growth spiral, and Bernoulli's spiral or spira mirabilis , this curve's rich properties have fascinated mathematicians since its discovery by 17th century philosopher Descartes . Intriguingly, this abstract shape is much more abundant in nature than suggested by the striking visual comparison above. Logarithmic spirals also describe, for example, the arrangement of sunflower seeds , the shapes of nautilus shells, and ... cauliflower . Pine cones Here is a picture of an ordinary pinecone seen from its base where the stalk connects it to the tree.

This pine cone shows the Fibonacci Spirals clearly. The number of spirals in either direction are two consecutive Fibonacci numbers.

You will occasionally find pine cones that do not have a Fibonacci number of spirals in one or both directions. Sometimes this is due to deformities produced by disease or pests but sometimes the cones look normal too. This article reports on a study of this question and others in a large collection of Californian pine cones of different kinds. The author also found that there were as many with the steep spiral (the one with more arms) going to the left as to the right. Pineapples and Fibonacci Numbers P B Onderdonk The Fibonacci Quarterly vol 8 (1970), pages 507, 508.
The Human Body 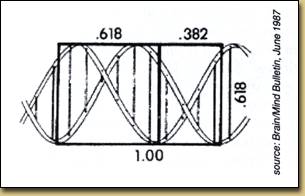
DNA fibonacci spiral structure
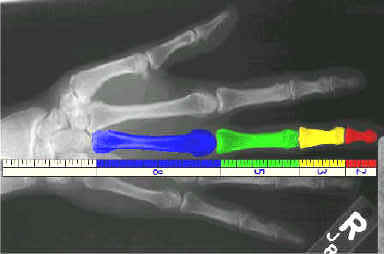
Human Hand 
Typical Human Body The golden ratio retains a mystique, partly because excellent approximations of it turn up in many unexpected places in nature. The spiral inside M51, the Whirlpool Galaxy, is remarkably close to the golden section, and the ratio of the lengths of the thorax and abdomen in most bees is nearly the golden ratio. Even a cross section of the most common form of human DNA fits nicely into a golden decagon. The golden ratio and its relatives also appear in many unexpected contexts in mathematics, and they continue to spark interest in the mathematical community.
For a review of the General Fibonacci series go to: