John R. Simmons

FINAL ASSIGNMENT

 

Part A. In this assignment we consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

 

 

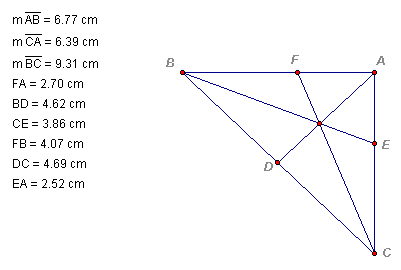
Now we explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

 

 

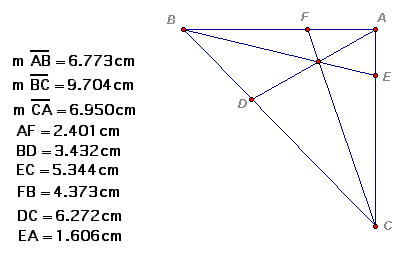
2.401*3.432*5.344=44.04, 4.373*6.272*1.606=44.04

As can be seen from the calculations above, when P is inside the triangle, the ratio of (AF)(BD)(EC) to (FB)(DC)(EA) is equal to 1.

 

Part B. Conjecture: In any triangle labeled as the one in Part A, with the point P inside the triangle, the ratio of (AF)(BD)(EC) to (FB)(DC)(EA) is always equal to 1.

 

Proof: By (The Theorem of Ceva). Given triangle ABC and a point P not on side AB or BC, or CA. If P is inside of triangle ABC, then all three point, D, E, F lie on the triangle, and (AF)(BD)(EC)/(FB)(DC)(EA)=1.

Further, if P is outside of triangle ABC then one and only of the three point D, E, F lies on the triangle.

Given triangle ABC and a point P not on line AB or BC, or CA. If the lines PA, PB, PC intersect lines BC, CA, AB at points D, E, F respectively then one and only one of the following statements is true: point F lies on side (AB) ie. (AFB), point D lies on side (BC) ie. (BDC), point E lies on side (CA) ie. (CEA).

Using Ceva's Theorem, we know the structure of all possible constructions involving point P and triangle ABC. Thus to generalize the the relationship we need only show that (AF)(BD)(EC)/(FB)(DC)(EA)=1 for any position of point P in the xy-plane except in one of the sides of triangle ABC.

The remainder of the proof follows.

 

Observe the illustrations below. With point P in regions 1, 2, 4, 6 the theorem holds. Similarly if point P is in any region outside of the triangle, one and only one of the three statements is true.

 

Figure 1

 

Figure 2

 

 

 

Figure 3

 

 

 

 

Figure 4

 

 

Figure 5

 

 

 

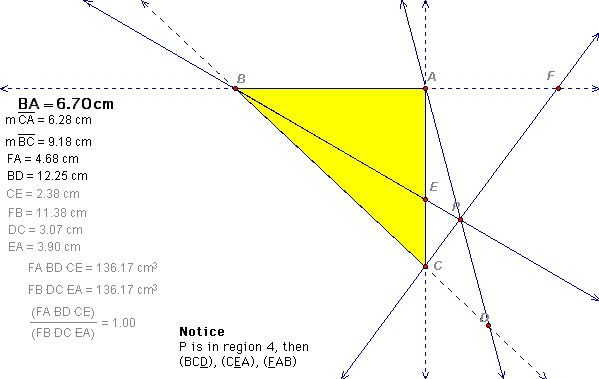
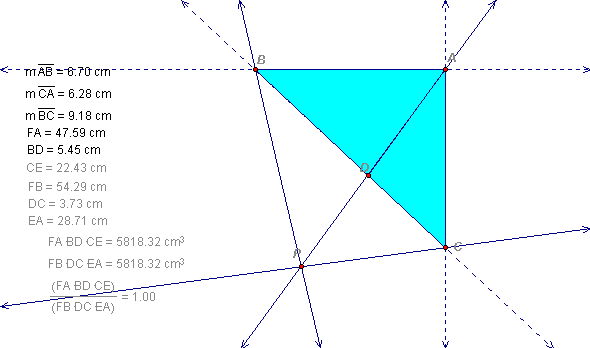
The remainder of the proof follows from similar triangles and the proportionality of their areas.

Figure 6

 

 

Figure 7

 

Figure 8

 

 

Figure 9

 

 

Figure 10

 

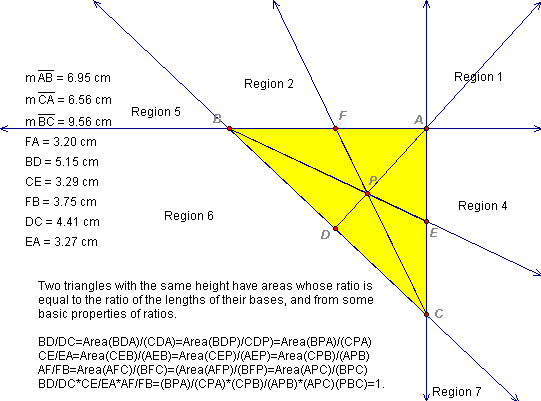
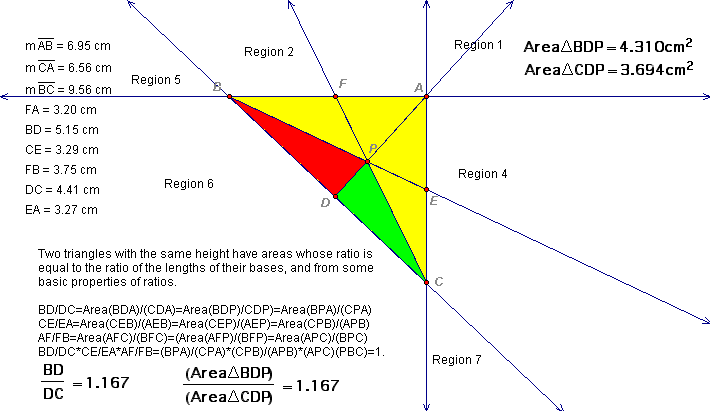
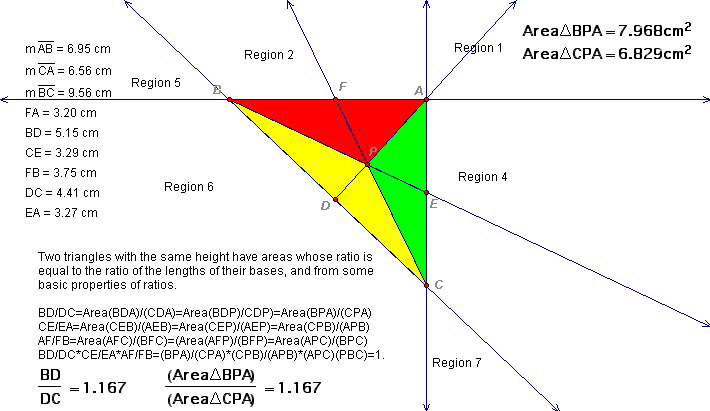
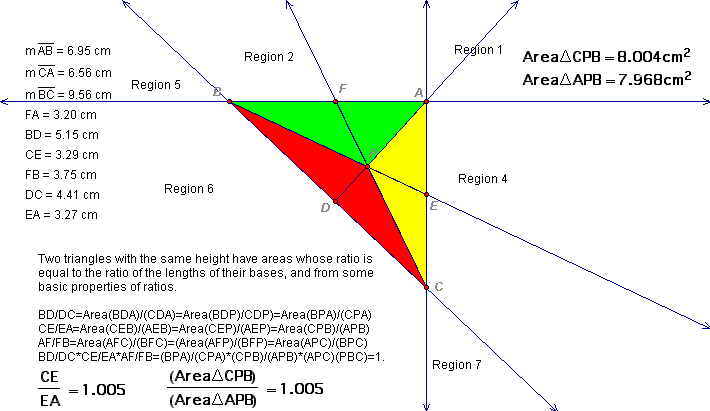
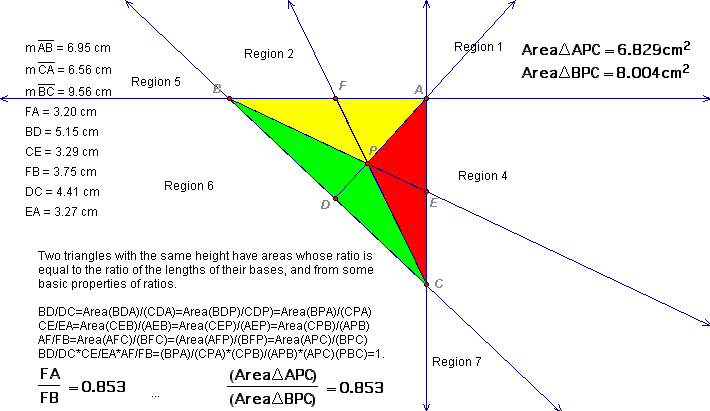
The next figure--(11)--summarizes our results and concludes the proof.

Figure 11

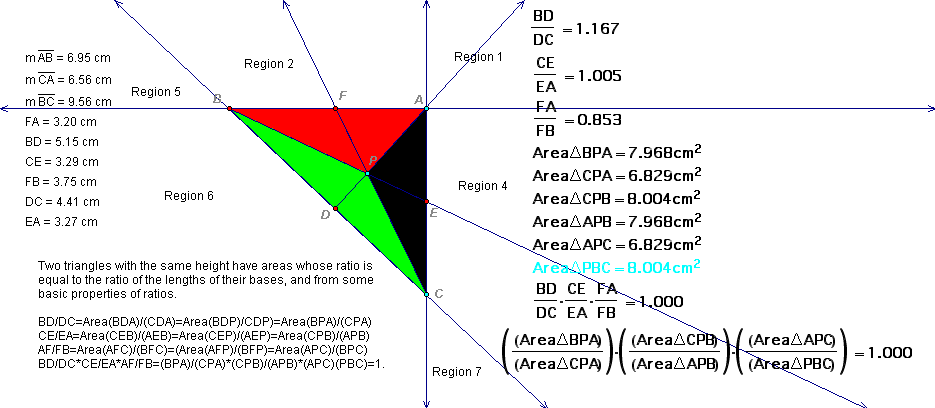
DONE//

 

Part C. When point P is inside triangle ABC, the ratio of the areas of triangle ABC and Triangle DEF is always greater than or equal to 4. To illustrate this we do some calculations of various relationships of this form.

 

Figure 12

 

Click here to manipulate point P.

 

In the next three figures we form the inner triangle using the points that bisect the sides of the larger triangle.

 

Figure 13

 

Figure 14

 

Figure 15

 

 

From our calculations we found that the ratio of the area of triangle ABC to inner triangle is equal to 4 when the inner triangle is formed by connecting segments that bisect the sides of the larger triangle.

 

 

Back to Main Page