This web page is intended to be a resource for teachers and students who want to go beyond the usual textbook treatment of conic sections. A bit of history, examples of applications, helpful websites, and demonstrations are included. Enjoy!

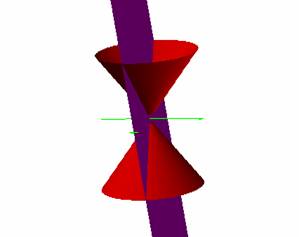The Ancient Greeks knew about the conic sections, the family of curves created when a plane slices through a cone. Menaechmus is credited with the discovery of conic sections in about 350 B.C. while he was trying to solve the problem of "doubling the cube" (Schmarge, 1999) . He observed that slicing a cone with a plane not parallel to its base would create certain curves, depending upon the angle at which the plane passes through the cone: circle, ellipse, parabola, hyperbola, point, line, or a pair of intersecting lines.  The point, line, and pair of intersecting lines are known as degenerate conics and occur when the plane passes through the vertex. If the plane passes through the vertex and is parallel to the bases, a point is the result; tangent to the cones, a line; and intersecting both cones, two intersecting lines.  You may want to investigate the intersecting lines - are they really just intersecting lines?

Watch the Cone demonstration. When you open this application, it is set up in such a way as to show the nondegenerate conic curves - circle, parabola, ellipse, and hyperbola. To see the degenerate conics - point, line, and intersecting lines - change 1 - nx to nx in the second and third equations so that the plane will be positioned at the center of the cone. It may be easier to see what is happening if you manually drag the slider instead of using the animation feature. When n < 1, the center point is the intersection of the cone and the plane. When n = 1 , the intersection is a line, y = 0. Dragging the cone around provides a better view of the plane for those values of n, but nothing will actually show on the 2-D graph. When n > 1 the intersecting lines will appear in the 2-D graph, representing the intersection of the cone and the plane. Compare the 2-D graph to the third equation. What can be said about y?

Although such famous Greek mathematicians as Euclid, Archimedes, Apollonius, and Pappas studied and wrote about the conic sections, it seems that the conic sections were more or less ignored until the sixteenth century, when once again, these interesting curves were explored. In about 1514, Copernicus distributed a little hand-written book, usually called the Little Commentary, in which he set out his theory about the universe. The book contained seven axioms, so called because Copernicus based his conclusions on these axioms and nothing else:

1. There is no one centre in the universe.
2. The Earth's centre is not the centre of the universe.
3. The centre of the universe is near the sun.
4. The distance from the Earth to the sun is imperceptible compared with the distance to the stars.
5. The rotation of the Earth accounts for the apparent daily rotation of the stars.
6. The apparent annual cycle of movements of the sun is caused by the Earth revolving round it.
7. The apparent retrograde motion of the planets is caused by the motion of the Earth from which one observes. (O'Connor & Robertson, 2002)

Johannes Kepler concluded in 1605 that the orbit of Mars was an ellipse with the Sun as one of its foci, a conclusion which was extended to all the planets and is now called Kepler's First Law of Planetary Motion. Kepler saw his theory as providing evidence for the Copernican theory, pointing out, for instance, that the Copernican theory could be used to explain why Venus and Mercury are never seen very far from the Sun whereas in the geocentric theory there was no explanation of this fact (Field, 1999) .

Kepler is thought to have coined the terms focus and directrix. Many students become familiar with these terms when they study conic sections, but the reflective properties of the conic sections –- the properties which make them important and which depend on the position of the foci and directrices- often receive little attention.

In the sketch shown here (International Educational Software, 1997) , parallel beams of light reflect on the parabola and gather at the focus; and light beams originating at the focus, directed at the parabola, will be reflected in a path perpendicular to the directrix. We are most familiar with this property as it is utilized in the design of flashlights and headlights. One of the more interesting observations of this reflective property involves a spoon, which is not usually a perfect parabola. If you look into a large spoon, you will see your image is upside down; but if you can get really close to the spoon –- use a really large spoon - your image will suddenly be right side up when you reach the "focus." Not only is this an interesting parabolic reflection, it is also a mirror that reverses things up and down rather than side to side! Investigate this parabola reflective property and its relationship with the position of the focus and the shape of the parabola by adjusting the coefficient A.

Most of us use parabolas every day. Satellite dishes, flashlights, headlights, and balls (parabolic path of projectiles) are a few examples. While not as frequently encountered as the parabola, the ellipse has real world utility, too. The reflective property of an ellipse is truly unique: any signal (light or sound) that starts at one focus is reflected to the other focus. Lithotripsy, a medical procedure for treating kidney stones, relies on this reflective principle. The patient is placed in an elliptical tank of water in such a way that the kidney stone is at one focus. High-energy shock waves, generated at the other focus, pulverize the kidney stone. Anyone who has had this treatment for a kidney stone is thankful for ellipses. The reflective properties of ellipses are also used in the construction of "whispering galleries," which are rooms in which a person can whisper near one focus and be heard at the other focus, even though he cannot be heard at many places in between (Britton, 2005) .

Hyperbolas also have important reflective properties, with any rays directed toward one focus of a hyperbola being reflected at the "hyperbolic mirror" to the other focus (International Educational Software, 1997) . These reflective properties have been important in the design of tracking systems, telescopes, and cameras. A sonic boom shock wave intersects the ground in part of a hyperbola, hitting every point on this curve at the same time such that people in different places along the curve on the ground hear it at the same time. Because the airplane is moving forward, eventually the boom will be heard by everyone in its path (Britton, 2005). You can see hyperbolas in the wake left by a motorboat and imagine how hyperbolas might be used in the field of optics, and one of the most interesting results of the reflective properties of hyperbolas is something we all love to see –- the most spectacular light show: a rainbow (Calvert, 2002) . Photograph (Wang, 2003) .

Frequently, students are first introduced to the conic sections by learning about parabolas and perhaps using the standard equation to graph the function, find the vertex, the axis of symmetry, the focus, and the directrix.

It is sometimes difficult to visualize the relationships between the parts of a parabola when it is just lying there on a piece of paper. Geometer's Sketchpad® enables students to see how a point on the parabolic curve is equidistant from the focus and the directrix regardless of the values of the coefficients (a, b, and c) in  construction of a parabola. Similarly, the ellipse and hyperbola can be graphed using the standard equations, and students can investigate the foci of these constructions. construction of an ellipse, construction of a Hyperbola (Woeppel, 2000) . Of course, conic Sections are not always centered at the origin, and their shapes do change - not every hyperbola looks the same! In this shifted conic construction, students can see how the coefficients affect the shape and location of the curves while the conic is oriented vertically or horizontally. In the rotated conic, the coefficient B alters that orientation.

The properties of the Conic Sections can be demonstrated by other construction methods as well, without relying on the equations to guide the construction. A fun exploration involves conics constructed from circles and a line. In these constructions of an ellipse and a hyperbola, students can see what is meant by a locus (shown in red), and what happens to the locus when the foci are moved (Davis, 2003). First, of course, it is necessary to understand the terms. A standard textbook definition of an ellipse says that any point is on an ellipse if the sum of the distance from that point to one focus and the distance from that point to the other focus equals 2a, where 2a is a fixed positive number greater than the distance between the two foci. Rarely is this statement explained. If we start with a circle, the two foci are actually the same point, the center of the circle, the radius of the circle is a, and the distance from the center to any point on the circle and back to the center is 2a. As the foci move away from each other, the circle becomes an ellipse, but the total distance from one of the foci to any point on the curve and then to the other focus is still 2a. A locus is a set of all points, or lines, that satisfy specific conditions; and in this case, the condition is that the sum of the distances from the two foci to the point is the constant 2a. An ellipse is simply the set, or locus, of points satisfying this total distance requirement. A hyperbola is defined as the locus of points such that the difference between these distances is a constant.

For the construction of the ellipse, we need to establish the constant length (sum or difference) that will be between the foci and the points on the ellipse. For the ellipse, we draw a segment and construct a point on the segment to divide it into two parts, each of which respresents the distance from one of the foci to the ellipse. Construct the two foci. Construct a circle centered at one focus, with radius the length of one part of the segment. Construct a second circle, centered on the other foci with radius the length of the other part of the segment. For the ellipse, construct the points of intersection of the two circles. The locus is shown on the sketch, and when you slide or animate the red button, the points of intersection will trace this path.The construction of the hyperbola is similar except that the defining segment has to be constructed in such a way as to represent the difference, rather than the sum, of distances. In the sketch, with the point O between the points N and P, NP - NO is this difference. Construct a circle with radius NP centered at one focus, and then another circle with radius NO, centered at the other focus. The intersection of these two circles (the blue circles) forms points on the hyperbola, but only half of the hyperbola is formed this way. Repeat the process, to construct the other half of the hyperbola, but reverse the order in which the foci are selected for the circle centers. The intersection of these two circles (the green circles) forms the other half of the hyperbola. Again, in the sketch provided, the locus is shown, and when you slide or animate the red button, the points of intersection will trace this path.

We can use perpendicular bisectors to construct the conic sections, beginning with the most basic circle construction by perpendicular bisector. The construction of an ellipse by perpendicular bisector starts with a circle, an arbitrary point inside the circle, and the perpendicular bisector of the segment from that arbitrary point to a point on the circle. In this construction, the arbitrary point inside the circle and center of the circle become the foci, and the perpendicular bisector is used to trace the ellipse. Note that you can erase the traces by selecting "erase traces" under the display tab. The hyperbola construction by perpendicular bisectors is similar, but in this construction the arbitrary point is on the outside of the circle. These sketches also show how the paper folding technique is used to create the conic sections. For example, to create an ellipse by paper folding, draw a circle with center A and place a point B anywhere in the interior of the circle. Fold point B onto any point on the circle, and repeat this step multiple times folding point B on the circle at as many different points on the circle as possible. Notice that each of the folds is the perpendicular bisector of the segment that could be drawn between B and the point on the circle.
You may have seen the sketch of the conic sections as the locus of perpendicular bisectors at the Key Curriculum Press web site (GSP locus sketch). You can create your own version of this dynamic conic and investigate the "envelope," or edges, of the locus that define the curve. This is simply the perpendicular bisector construction method set up in such a way that you can move one of the foci and see the changes that occur in the sketch as the focus is moved from the interior of the circle to the exterior of the circle.

The eccentricity of a Conic Section measures its distortion from a circle - for a circle, the eccentricity would be zero because there is no distortion. When we define the conic sections in terms of their eccentricity, we are referring to a constant ratio between the distance from a focus to a point on the conic to the distance from that same point on the conic to the directrix. Rectangular coordinates emphasize the location of the center of the conic whereas using polar coordinates places the emphasis on the location of the foci. Since most applications of the conics involve their reflective properties, and the reflective properties involve the foci, it makes sense to define conics in terms of their eccentricity. (Sparknotes, 2005) . To see how to arrive at the equation of the conic section in polar form, open construction of conic section in polar coordinates. (Arnold, 1999) Note the effect of changes in eccentricity on the conic section: when the eccentricity is less than 1, the curve is an ellipse, when the eccentricity equals 1, the curve is a parabola, and when the eccentricity is greater than 1, the curve is a hyperbola.

In another construction with eccentricity the eccentricity changes as we would expect, but the ratio has been calculated using the ratio between the distance between the two foci, one of which is the center of the construction circle, and the distance from the center of the circle to a point on the circle. How can we establish the validity of this calculation? In this sketch there is no directrix to use in calculating the eccentricity, but one definition of eccentricity is the ratio of the distance between the foci and the major axis. In this construction, the length of the major axis (the distance between the vertices of the conic) is equal to the radius of the circle.

An interesting construction using tangent circles provides an opportunity for some additional exploration into the properties of the conics as well as properties of triangles. In this sketch, circumcenter CC has been constructed for the pink triangle, which is just one of many possible triangles you could construct. Notice the behavior of circumcenter CC as the eccentricity changes – you might want to construct a locus (circumcenter CC and the pull point) and try to figure out why it follows the particular path that it follows. Think about the other "centers" of the triangle. What might happen to them? You can construct those centers and trace them to see if there are any interesting patterns as well as finding interesting triangles and patterns of your own (Daly, 2003). You might want to investigate construction of conics from the centers of various triangles - here is one example. If this conic construction looks a bit strange to you, see exactly how it was done in the tangent circle conic construction sketch.

Clearly, there are many ways to explore the family of curves known as conic sections as well as the relationships between these curves and other geometric shapes. We've constructed conic sections using their equations, their foci and directrices, and we've created them using cones, planes, lines, and circles. There are rich and powerful mathematical relationships embedded in these seemingly simple curves, and the possibilities for investigations are virtually endless. Enjoy!

2005

Suggestions or comments?

References

Arnold, D. (1999). The Conic Sections in Polar Coordinates. Retrieved 5/22/2005, from http://online.redwoods.cc.ca.us/instruct/darnold/MultCalc/PolarConics/conics.htm

Britton, J. (2005). Occurrence of the Conics. Retrieved 5/25/2005, from http://britton.disted.camosun.bc.ca/jbconics.htm

Calvert, J. B. (2002). Hyperbola. Retrieved 5/31/2005, from http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Kepler.html

Daly, W. (2003). Playing with Tangent Circles. Retrieved 5/23/2005, from http://jwilson.coe.uga.edu/EMT668/EMAT6680.2003.Su/Daly/Write_Ups/WR_7/Asmt_7.htm

Davis, A. (2003). Conic Sections. Retrieved 5/23/2005, from http://www.auburn.edu/~davisak/wu2hyperbola.htm

Field, J. V. (1999). Johannes Kepler. Retrieved 5/24/2005, from http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Kepler.html

International Educational Software. (1997). Conics. Retrieved 5/24/2005, from http://www.ies.co.jp/math/java/conics/

Math Pages.Pascal's Mystic Hexagram. Retrieved 5/26/2005, from http://www.mathpages.com/home/kmath543/kmath543.htm

O'Connor, J. J., & Robertson, E. F. (2002). Nicolaus Copernicus. Retrieved 5/24/2005, from http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Copernicus.html

Schmarge, K. (1999). Conic Sections in Ancient Greece. Retrieved 5/31/2005, from http://www.math.rutgers.edu/~cherlin/History/Papers1999/schmarge.html

Sparknotes. (2005). Polar Form of the Conics, from http://www.sparknotes.com/math/precalc/conicsections/section6.rhtml

Wang, R. (2003). Rainbows, from http://www.cs.princeton.edu/~rywang/berkeley/magic_small/rainbows.html

Woeppel, J. J. (2000). Constructions using Geometer's Sketchpad, from http://portfolio.iu.edu/jwoeppel/M110/ClassAssignment6.htm

The content and opinions expressed on this Web page do not necessarily reflect the views of nor are they endorsed by the University of Georgia or the University System of Georgia .