Instructional Unit
Trigonometric Functions
I made a instructional unite about trigonometric functions. I start with the definition of trigonometry functions. Our final goal is to show the graphs of sin(x), cos(x), and tan(x) by means of GSP. In my teaching unite, there are several exercises that students learn as their home work or their classroom assessment.
Ā@
Day1, 2, 3, and 4
Introduction and sone basic ideas of trigonometric functions with a right triangle
Ā@
Day 5, 6, 7, and 8
Trigonometric functions with a unite circle
Ā@
Day 9 and 10
The graphs of sin(x), cos(x), and tan(x) shown by GSP.
Day1
Investigation of similar triangles
Ā@
<Examples>

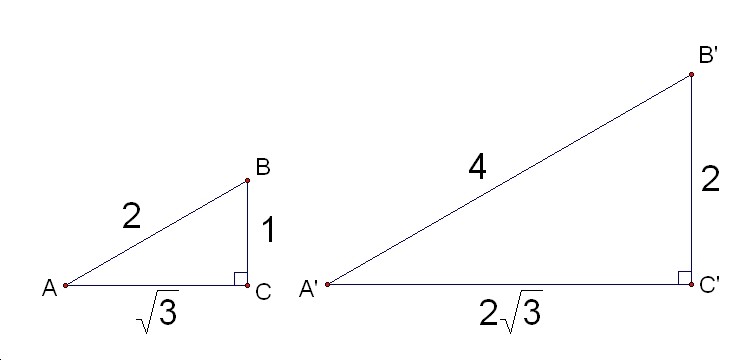
Two triangle ABC and A'B'C' are similar. Think about the ratios of each two sides of a right triangle.
Question: What are AC/AB and A'C'/A'B'? What are BC/AB and B'C'/A'B'? What are BC/AC and B'C'/A'C'? Compare the result.
Result:
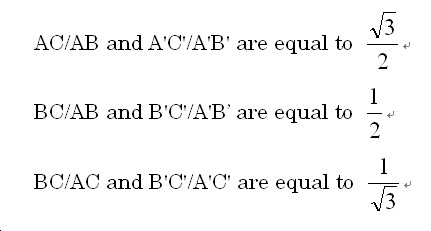
The two similar triangles have the same ratios of two sides.
Ā@
Try on another two right triangles.
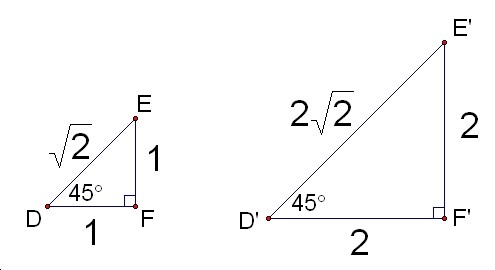
Think about the ratios of each two sides of a right triangle.
Question: What are DF/DE and D'F'/D'E'? What are EF/DE and E'F'/D'E'? What are EF/DF and E'F'/D'F'? Compare the result.
Result:

The two similar triangles have the same ratios of two sides.
We observe that similar right triangles have the same ratios of each two sides. Another thing we got as a result is that if two right triangles are not similar, they have different ratios of each two sides.
Here we start thinking of the relationship between the angle and the ratios of two sides of a right triangle.
Ā@
Definition of trigonometric functions
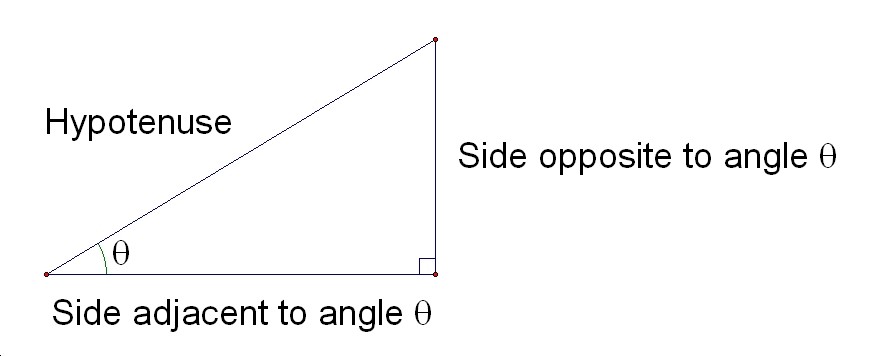

Exercise
Calculate and compare the values of sinÉ∆, cosÉ∆, and tanÉ∆for both triangle below.
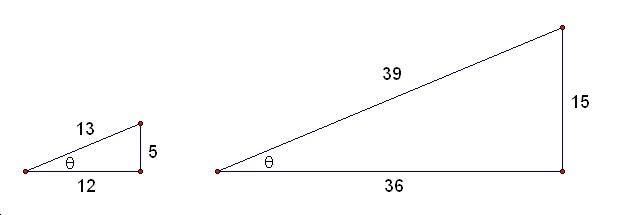
Day2
Trigonometic values with various angles
Ā@
In this day we start over with an exercise problem in order to review and prepare for intrducing new concept.
Ā@
Exercise
Calculate the values of sinÉ∆, cosÉ∆, and tanÉ∆, where É∆= 30Āč, 45Āč, 60Āč
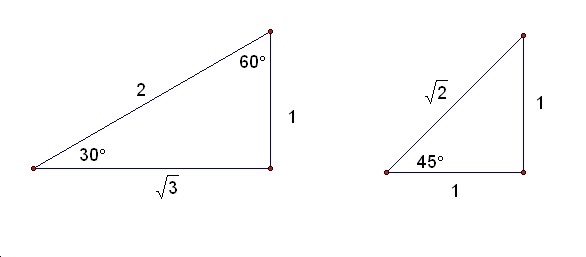
Think about this problems for some right triangles with various lengths.
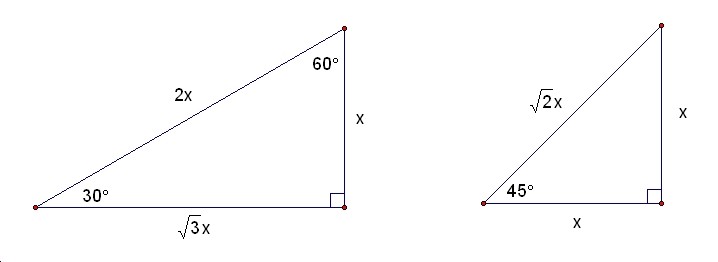
The answer of this problems are below.
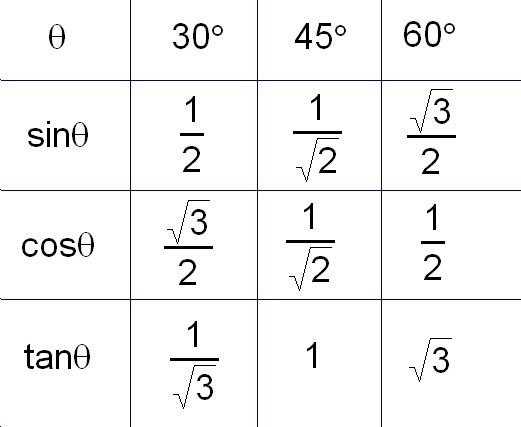
Different angles give different values of sinÉ∆, cosÉ∆, and tanÉ∆. sinÉ∆, cosÉ∆, and tanÉ∆ depends on an angle.
We are familiarized with the right triangle of angles 30Āč, 40Āč, and 60Āč. How about a triangle with other angles between 0Āčand 90Āč? It is hard to find values for most other angles. By spread sheet, we can look at how sinÉ∆, cosÉ∆, and tanÉ∆ are changing to É∆. The values shown in the cells are apploximation of the values.
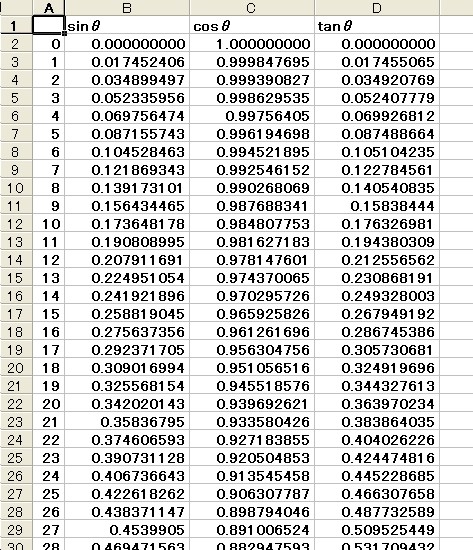
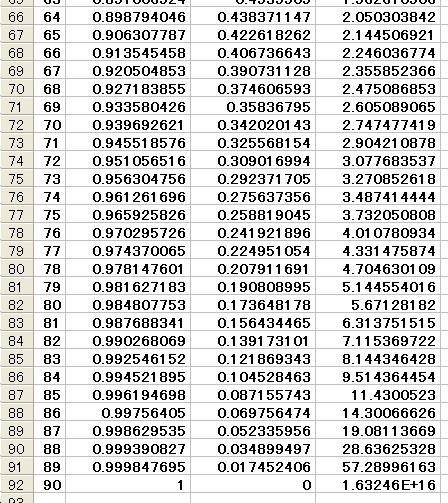
Think of each value of sinÉ∆, cosÉ∆, and tanÉ∆whenÉ∆= 90Āč or 0Āč. We need to extend the definition of trigonometric function for considering the case that É∆is not between 0 Āčand 90Āč.
Exercise
What is sin63Āč?
What is cos19Āč?
Ā@
Exercise
What is an angle A so that sinA=0.39?
What is an angle A so that cosA=0.53?
Day3
Application of sinÉ∆, cosÉ∆, tanÉ∆.
Ā@
Why people made the trigonometric functions? How useful are they? One obvious application of them to the real world is measurement of some length. Consider the problem below.
Ā@
A helicopter hovers 800 ft directly above a small island that is off the California coalst. From the helicopter, the pilot takes a sighting to a point P directly ashore on the mainland, at the water's edge. If the angle of depression is 35Āč, how far off the coast is the island?

Solution
Let x denote the distance from the island to the mainland. Then, as you can see from Figure 7, we have É∆+35Āč=90Āč, from which it follows that É∆=55Āč. Now we can write
tan55Āč=x/800
or
x= 800 tan55ĀčĀŗ1150 ft
(using a calculator and rounding to the nearest 50 feet)
Ā@
Ā@
Exercise
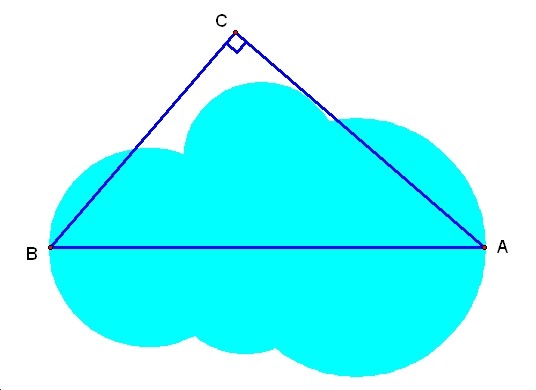
Determine the distance AB across the lake shouwn in the figure, using the following data: AC=400m, ĀŕC=90Āč, and ĀŕCAB=40Āč.
Day4
Relationship between trigonometric values shown with a right triangle.
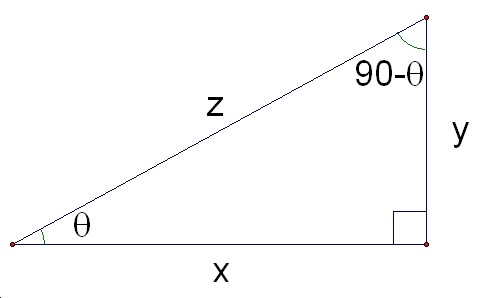
By the difinition, define each trigonometry value for two angles É∆ and 90-É∆ of the triangle above and compare the values.
Result:
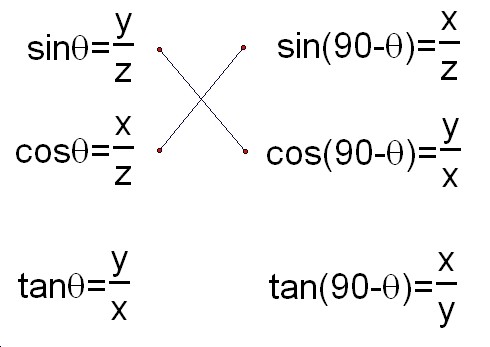
Thus, we got below relationship between one with É∆and one with 90-É∆.
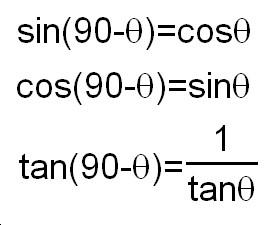
Exercise
Use an angle smaller than 45 to express each below
sin75Āč
cos65Āč
tan 72Āč
Day5
(cosÉ∆, sinÉ∆)on the unite circle
Ā@
We need to give new definitions of sinÉ∆ and cosÉ∆ to think of the case of É∆>90.
Ā@
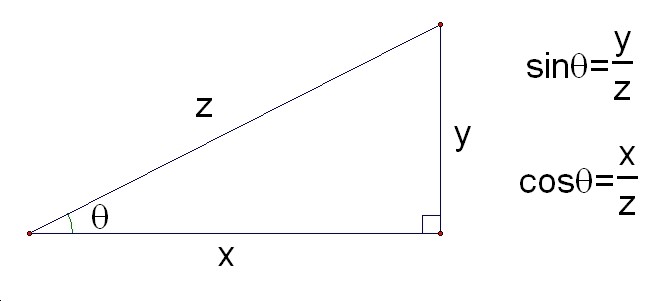
Step1
Think of a right triagnle, review the difiniton of sinÉ∆and cosÉ∆.
Step2
If the length z is equal to 1, sinÉ∆is equal to y and cosÉ∆is equal to x like below.
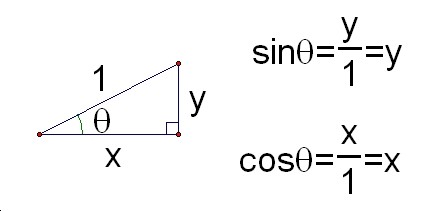
Step3
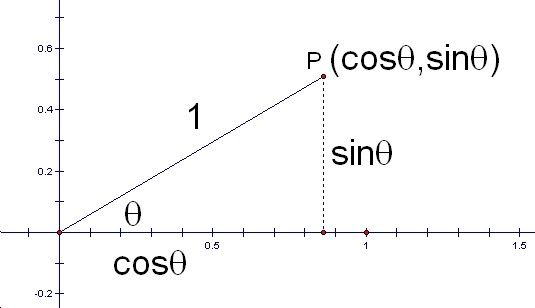
Consider the point with interior angle É∆ is on the origin point on xy plane. Then, since the two smallest sides are sinÉ∆and cosÉ∆, the point P in above picture has a coordinate (sinÉ∆, cosÉ∆).
Ā@
Step4
The coordinates of point P changes as the angleÉ∆changes between 0Āčand 90Āč.
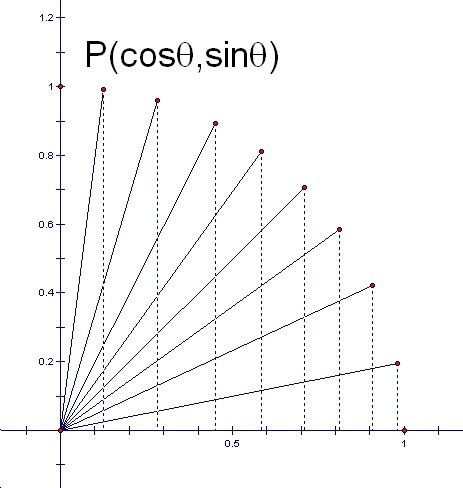
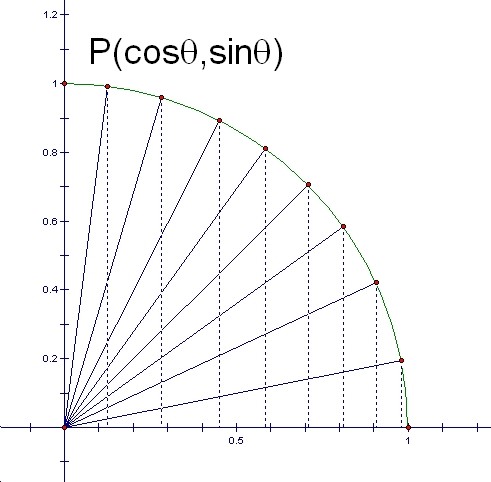
It seems that the point P is on a circle.
Ā@
Step5
Even if É∆is greater than 90Āč, we can define the value of cosÉ∆and sinÉ∆ as the coordinates of the point P.
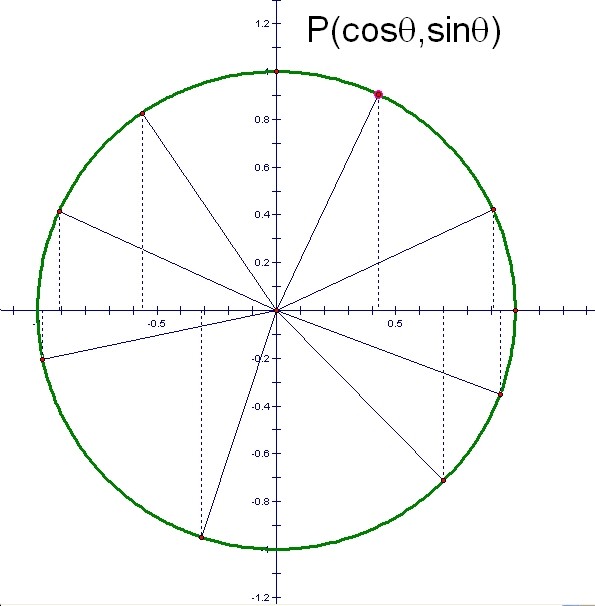
The angle É∆can be any angle between 0Āčand 360Āč(actually, any big angle greater than 360Āč or any negative angle), Whatever É∆is, the value of sinÉ∆ and cosÉ∆ is the coordinates of the point P.
Ā@
Excercise
find the value of sinÉ∆ and cosÉ∆ for each angle below.
É∆=0Āč, 90Āč, 120Āč, 180Āč, 225Āč, 300Āč.
Day6
Relationship between trigonometric values shown with the unite circle (1)
Ā@
Let us continue to deal with value of sinÉ∆ and cosÉ∆ with many different angles of É∆. Here is a work sheet for students to fill the value of trigonometric funcion for each angle between 0 and 360.
| É∆ | 0 | 30 | 45 | 60 | 90 | 120 | 135 | 150 | 180 | 210 | 225 | 240 | 270 | 300 | 315 | 330 | 360 |
| sinÉ∆ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ |
| cosÉ∆ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ |
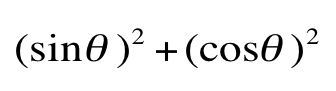 |
Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ | Ā@ |
It is not important to fill all the cell of this table but to
think about what is in each of the very bottom cells. While filling this table,
especially the very bottom cells, we may realize in a short time that ![]() .
The reason of equation is very obvious. It is because that cosÉ∆and sinÉ∆are each
of the coordinates of a point on the circle with its center of the origin, that
is (0, 0) and with its radius of 1.
.
The reason of equation is very obvious. It is because that cosÉ∆and sinÉ∆are each
of the coordinates of a point on the circle with its center of the origin, that
is (0, 0) and with its radius of 1.

It is easy to see this with spread sheet like below.
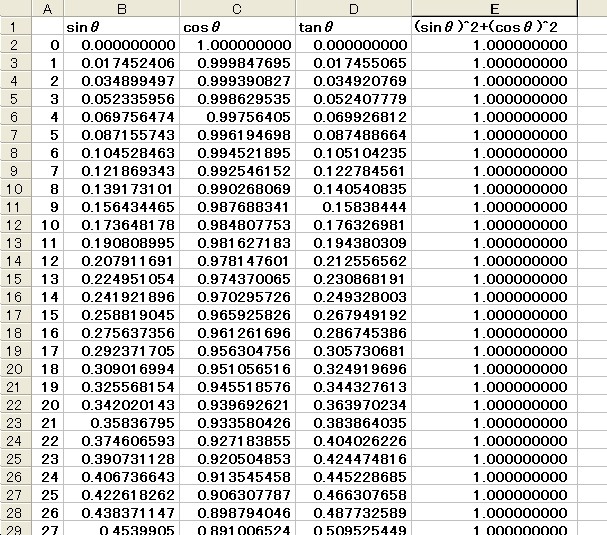
Can you find any other relationship between them? How about tanÉ∆?
Actually, tanÉ∆ has a property expressed with sinÉ∆ and cosÉ∆like below.
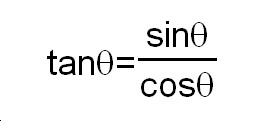
The proof of this is not so easy but not so complicated eather. Think about a right triangle again.

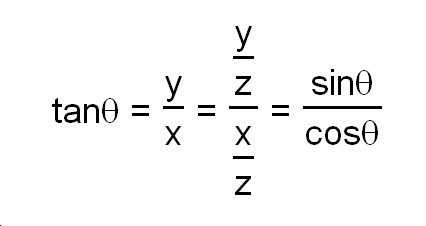
Usining this result(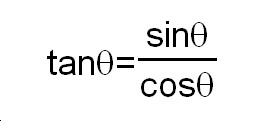 ),
we can obtain another equation of tanÉ∆and cosÉ∆, starting on
),
we can obtain another equation of tanÉ∆and cosÉ∆, starting on![]() .
.
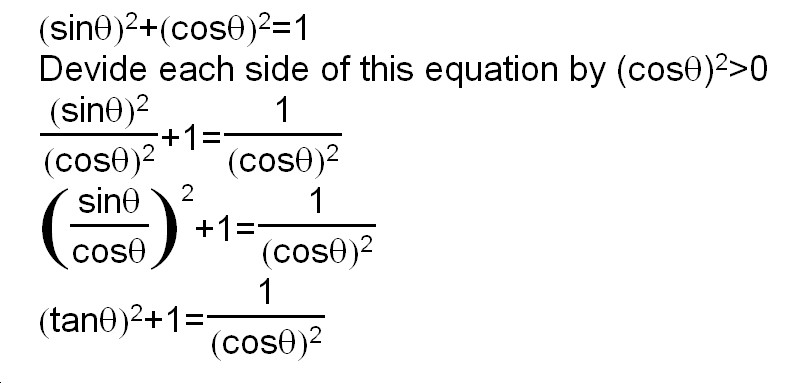
Ā@
Exercise
When cosÉ∆=-3/4 and 0<É∆<180, find sinÉ∆ and tanÉ∆.
Day7
Relationship between trigonometric values shown with the unite circle (2)
Ā@
Now we can discuss trigonometric functions with an angle greater than 90Āč and we know that
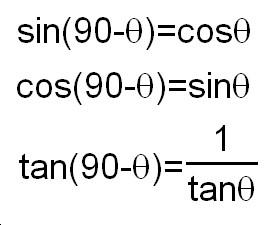 .
.
Let us see what happens if we change the minus sigh into plus
sign. I mean, think about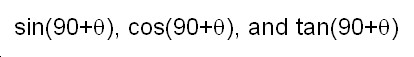 .
.
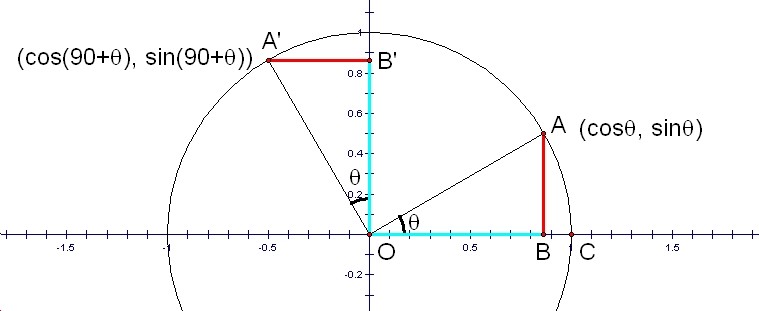
In this picture, the point A and the point A' has an angle É∆and 90Āč+É∆ respectively. Thus, the coordinates of A is (cosÉ∆,sinÉ∆) and the coordinates of A' is (cos(90+É∆), sin(90+É∆)). Because the triangle AOB and the triangle A'OB' are similar, the each pair of the sides colored blue and red has the same length.
Finally, paying much attention to signs, we get 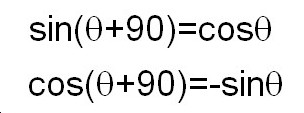
Next, I need to deal with tan(90+É∆). Using the result we have got, we can change tan(90+É∆) into a simple form with É∆, like below.
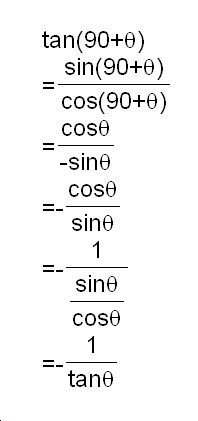
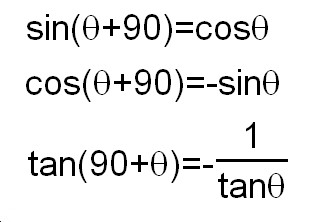
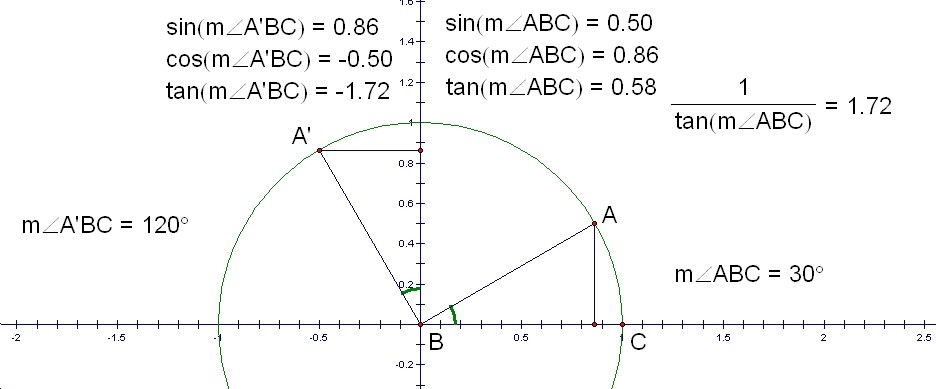
Here is a GSP file I made to show this trigonometric relationship.
Exercise
Consider the followings. Express them only with É∆.
sin(180+É∆)
cos(180+É∆)
tan(180+É∆)
sin(180-É∆)
cos(180-É∆)
tan(180-É∆)
sin(270+É∆)
cos(270+É∆)
tan(270+É∆)
sin(270-É∆)
cos(270-É∆)
tan(270-É∆)
sin(360+É∆)
cos(360+É∆)
tan(360+É∆)
sin(360-É∆)
cos(360-É∆)
tan(360-É∆)
Day8
Value of tanÉ∆around the unite circle
Ā@
A pair (cosÉ∆, sinÉ∆) is a coordinates of a point on the unite circle. How about tanÉ∆? Where is it around the unite circle? Think about this by starting over an right triangle again.
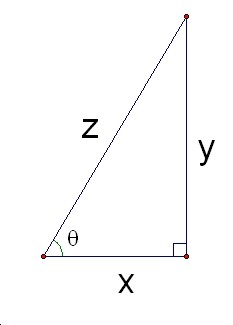
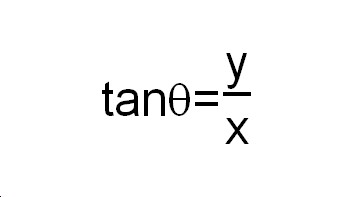
If the length x is equal to 1, then the length y is equal to the length y.
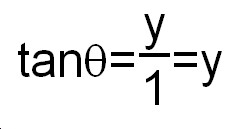
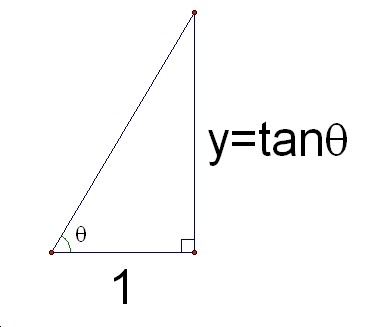
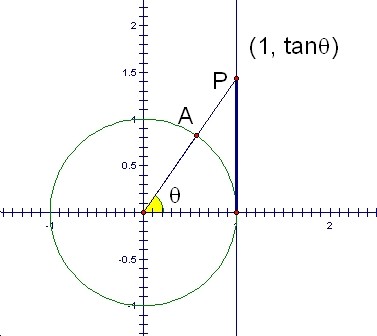
Thus, we have found the value of tanÉ∆ within the unite circle, as the y-coordinate of the point P on the line that is x=1. Note that the base of the triangle is 1.
Even when the angle É∆is more than 90Āč, tanÉ∆is defined as the y-coordinate of the pointP on the line x=1
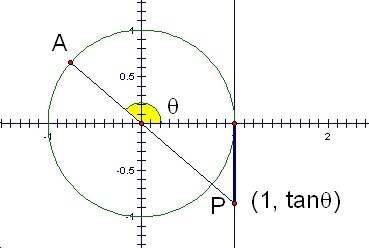
Note: The length of the thick segment is the absolute value of tanÉ∆.
Ā@
Exercise
Make it sure that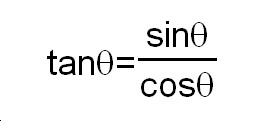 is correct when 0<É∆<360.
is correct when 0<É∆<360.
Day9
The graph of y=sin(x)
Ā@
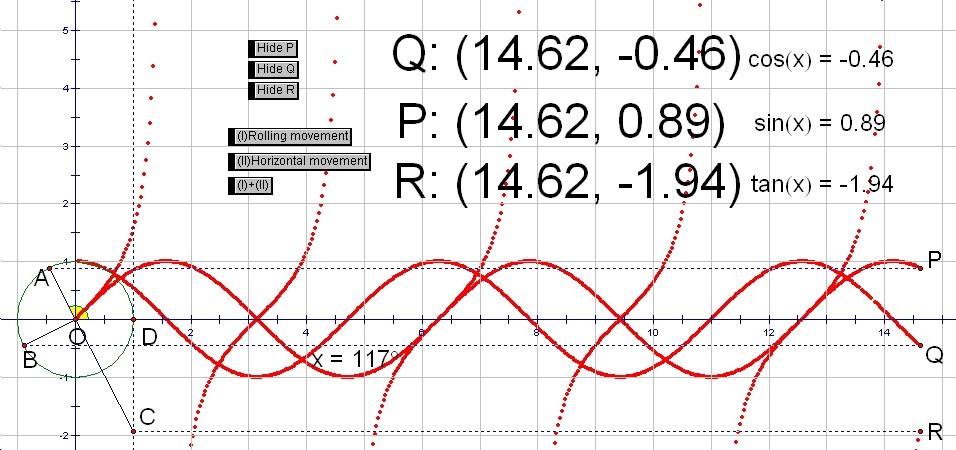
In this part of our lessen, we show by a GSP file (Click here to download this file) students how to draw the graph of sin(x) .
In the file, there are three bottons,
(I)Rolling movement, (II)Horizontal movement, and (I)+(II).
Ā@
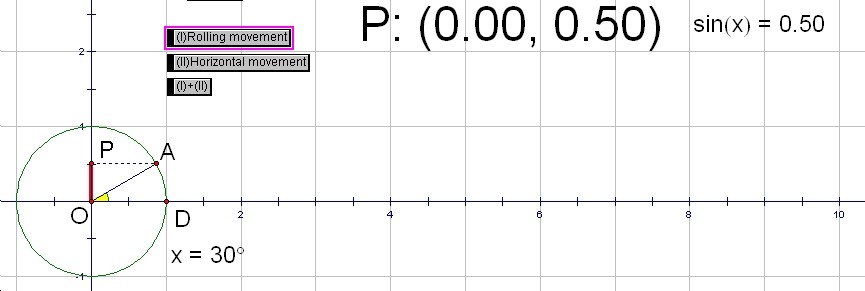
If you push the button (I), the point A moves around on the unite circle and the point P also moves on y-axis along with the point A.
Stop the movement of button (I). Then, if you push the button (II), the point P moves right horizontally.
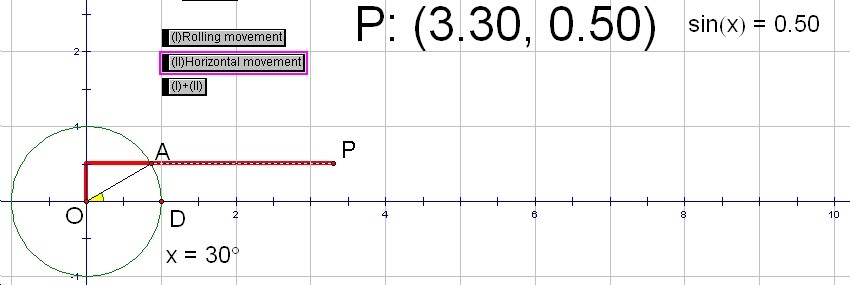
Go back to the first position (and erace traces). If you push the third button (I)+(II), the point A moves around and the point P moves horizontally at the same time. As a result, a curve like a wave appers. This curve is a graph of y=sin(x).
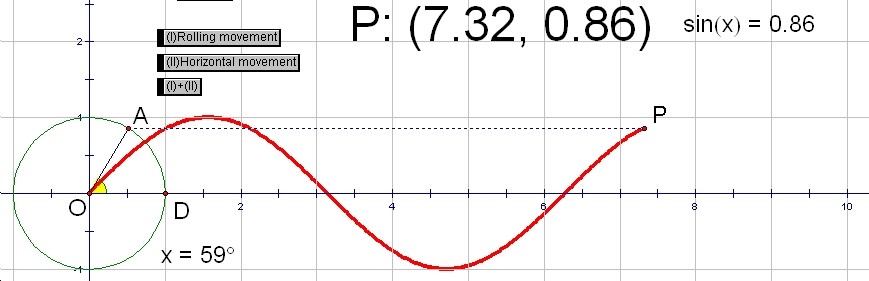
ĀŕAOD is transformed into the value of x in y=sin(x).
Ā@
Exercise
Change the starting position of the point A, P, or both. Try various positions of the points and interprete the curve of a result.
Consider an equation y= sin(ax+b). How does this graph change if a and b changes independently.
Day 10
Ā@
The graph of y=cos(x)
Because cosÉ∆=sin(É∆+90), the graph of y=cos(x)(=sin(x+90)) starts at the point with the coordinates (0, 1). If you push the button (I), the point Q goes down on the y-axis as the point B moves around on the unite circle.
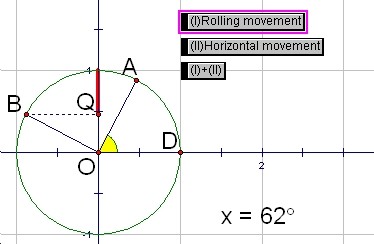
IF you push the button (I)+(II), the point Q leads a curve, which is the graph of y=cos(x).
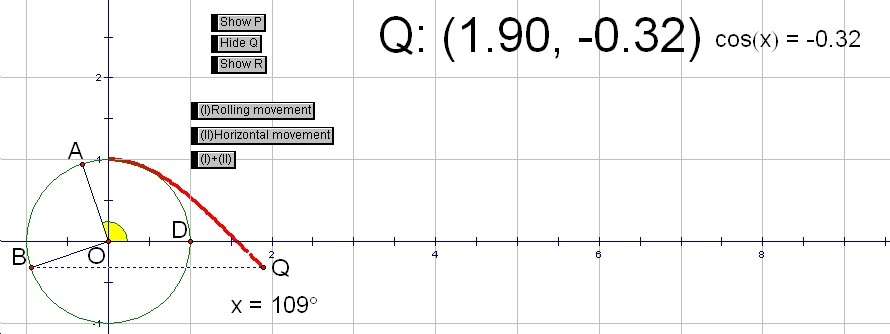

Ā@
The graph of y=tan(x)
The value of tan(x) is the y-coordinate of the point C on the line x=1. The point R goes up along with the point C as the point A moves around on the unite circle.
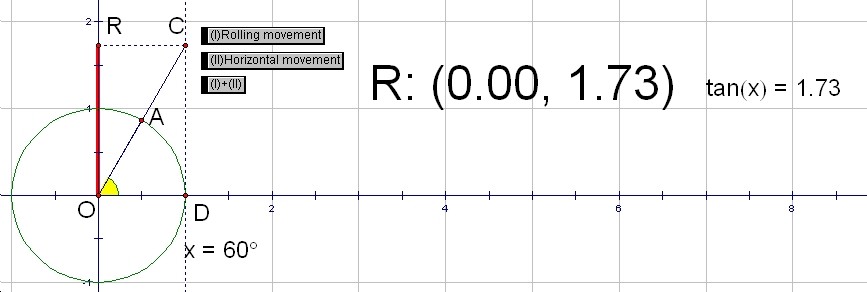
If you push the button (I)+(II), the graph of y=tan(x) appears behind the point R.
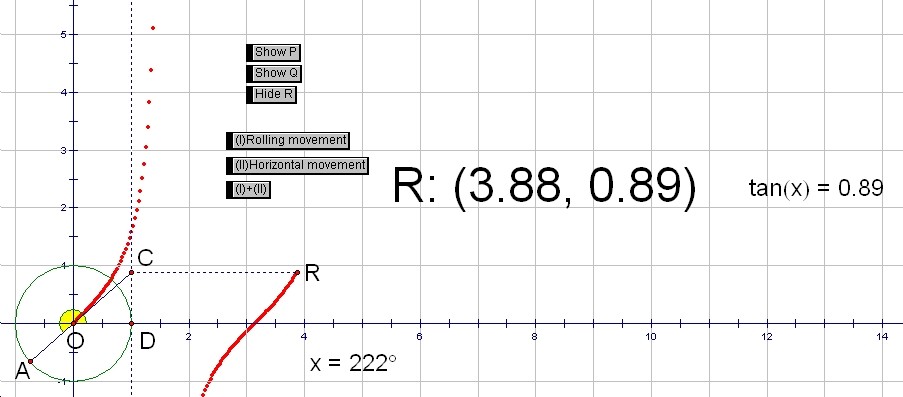
We can see that when É∆is 90Āč, 270Āč, 450Āč, ... the value of tan(x) does not exist.
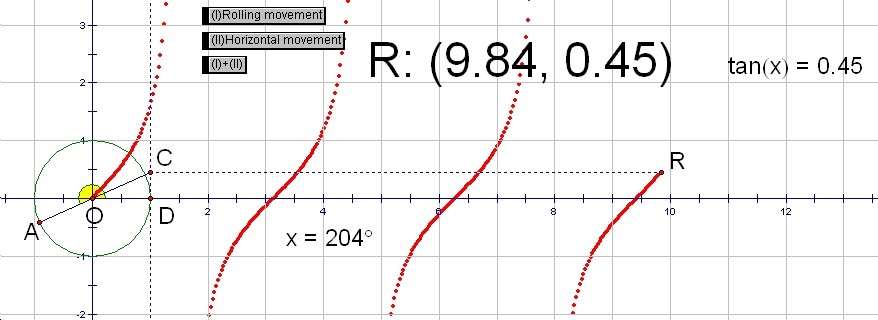
Ā@
Ā@
Exercise
Where each two graphs of the tree intersect? What is the angle giving the intersections? Why?