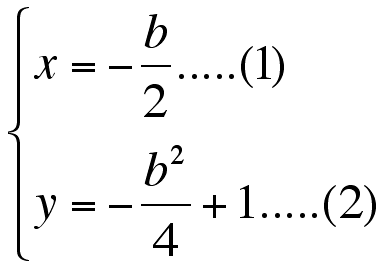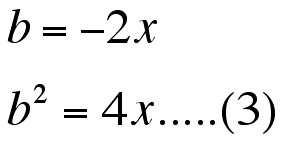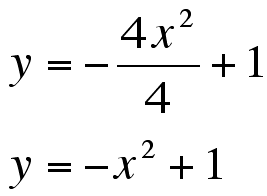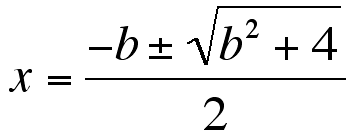Assignment3
investigation 1
I look for the coordinates of the vertce
of the parabora,
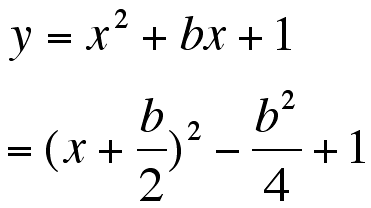 So, the coordinates of the vertice
is
So, the coordinates of the vertice
is 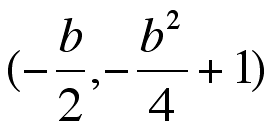 .
.
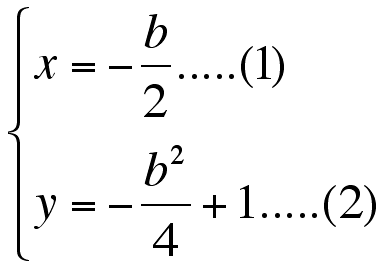 I make an equation by using this simultaneous
equqtions.
At first, I change (1).
I make an equation by using this simultaneous
equqtions.
At first, I change (1).
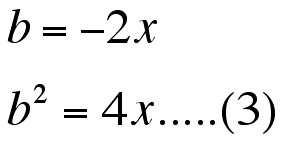 Next, substitute (3) for (2)
Next, substitute (3) for (2)
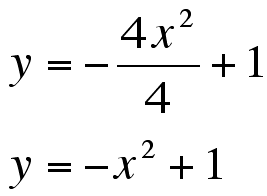 This is the result desired, the locus
of the vertices.
In general, the locus of the vertices
of
This is the result desired, the locus
of the vertices.
In general, the locus of the vertices
of 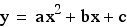 is
is
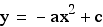
investigation2
Here are the graphs 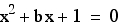 (Purple)
and
(Purple)
and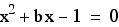 (red)
It is clear that, for any b,
(red)
It is clear that, for any b, 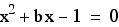 has two intersection points with a horizontal
line. This means that we get two real roots of
has two intersection points with a horizontal
line. This means that we get two real roots of 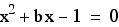 ,
one is positive and the another is negative.
we can calucurate this roots as below,
,
one is positive and the another is negative.
we can calucurate this roots as below,
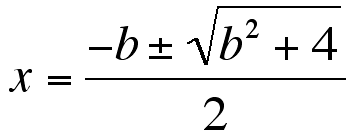 that are always real numbers.
I show 7 graphs for 7 values of c as
-3, -2, -1, 0, 1, 2, 3.
When c is positive, the graph exists
the 2nd quadrant and the 4th quadrant separately.
When c is negative, the graph exists
on the left of b-axis(the area where x < 0) and the right
of b-axis(the area where x > 0) separately.
When c = 0, the graph is a line throuh
the origin.
that are always real numbers.
I show 7 graphs for 7 values of c as
-3, -2, -1, 0, 1, 2, 3.
When c is positive, the graph exists
the 2nd quadrant and the 4th quadrant separately.
When c is negative, the graph exists
on the left of b-axis(the area where x < 0) and the right
of b-axis(the area where x > 0) separately.
When c = 0, the graph is a line throuh
the origin.
investigation3
I draw the graphs,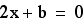 ,
,
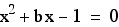 , and
, and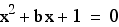 on
the same axex.
The graph
on
the same axex.
The graph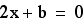 has
two intersection points with the graph
has
two intersection points with the graph 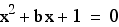 (red)
and no intersection point with the graph
(red)
and no intersection point with the graph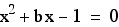 (purple).
This means that there are two sets(x,
b coordinates) of real roots for the simultaneous equations
(and that there is no real root for
the set of equations
The two sets of real roots are (x,
b) = (1, -2) and (-1, 2). These are the points where the graphs
intersect.
(purple).
This means that there are two sets(x,
b coordinates) of real roots for the simultaneous equations
(and that there is no real root for
the set of equations
The two sets of real roots are (x,
b) = (1, -2) and (-1, 2). These are the points where the graphs
intersect.
investigation4
On xc plane, I show 7 graphs of
All of the graphs are going through
the origin.
The locus of vertices is a parabora
Here I show you the animation of the
moving graph
when b = 0, we get one root of the
equation with the line c = 0.
When b is not equal to 0, we get two
roots of the equation with the line c = 0.
investigation5
On xa plane, I show 7 graphs of 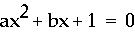 for 7 values b as -3, -2, -1, 0, 1, 2, 3.
Where x = 0, the graph does not exist.
In this case, there is no root of the equation with the line a
= 0.
For any b, when the value of x goes
to the infinity or negative infinity, the value of a approaches
to 0.
Here I show you the animation of the
moving graph
for 7 values b as -3, -2, -1, 0, 1, 2, 3.
Where x = 0, the graph does not exist.
In this case, there is no root of the equation with the line a
= 0.
For any b, when the value of x goes
to the infinity or negative infinity, the value of a approaches
to 0.
Here I show you the animation of the
moving graph 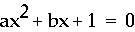 ( b changes from -5 to 5).
The graphs have two parts, the right
part and the left part.
The right and left graph are same shape
when b = 0.
The right part is shaped like a mountain
when b is negative.
The left part is shaped in this way
when b is positive.
For any b except for b = 0, we get
exact one root of the equation with the line a = 0.
( b changes from -5 to 5).
The graphs have two parts, the right
part and the left part.
The right and left graph are same shape
when b = 0.
The right part is shaped like a mountain
when b is negative.
The left part is shaped in this way
when b is positive.
For any b except for b = 0, we get
exact one root of the equation with the line a = 0.
Investigation6
On xb plane, I construct a movie of
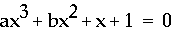 (a changes from -5 to 5).
The number of roots of this equation
with the line b = 0 is one, two, or three.
Can you see the graph having three
roots?
Next, on xc graph, I show a movie of
(a changes from -5 to 5).
The number of roots of this equation
with the line b = 0 is one, two, or three.
Can you see the graph having three
roots?
Next, on xc graph, I show a movie of
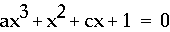 (a changes from -5 to 5.).
The number of roots of this equation
with the line c = 0 is 0 (when a = 0) or one.
(a changes from -5 to 5.).
The number of roots of this equation
with the line c = 0 is 0 (when a = 0) or one.
On xd graph, I make a movie of 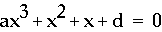 (a changes from -5 to 5).
All the graphs are go through the origin
(0, 0).
The number of roots of this equation
with the line d = 0 is one, two(when a = 0), or three.
(a changes from -5 to 5).
All the graphs are go through the origin
(0, 0).
The number of roots of this equation
with the line d = 0 is one, two(when a = 0), or three.
return
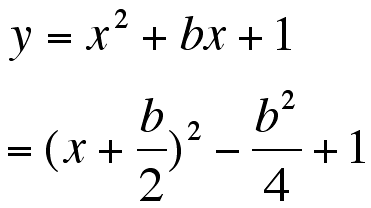
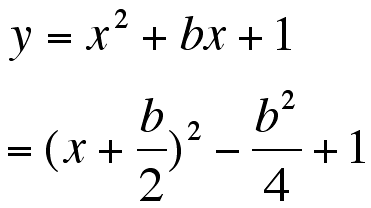
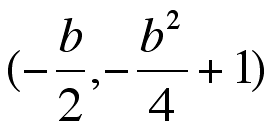 .
.