Assignment8
I did the first 6 constructions.
The Orthocenter of triangle HBC is A. (This
is obvious. The Orthoecenter of triangle HBC is on the intersection
of AB and AC because the perpendicular line through B to CH is
AB, and the perpendicular line through C to BH is AC)
The Orthocenter of triangle HAB.is C (the same
reason as above)
The Orthocenter of triangle HAC is B (the same
reason as above)
The circle C1 is go through A, B and
C.
The circle C2 is go through H, B and
C.
The circle C3 is go through H, A and
B.
The circle C4 is go through H, C and
A.
Radius of ABC, ABH, BCH, and CAH are
same lengh.
You make sure this by seeing this
GSP file(click here).
In addition, the area of ABC and the
area of the triangle made by using the three centers as its vertexes.
The two triangles (ABC and O2O3O4)
are congruent because O3O4 and BC are parallel, O3O2 and CA are
parallel, and O4O2 and AB are parallel.
You can click
here to see the file.
I found that 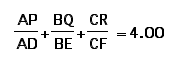 ,
I do not have any proof of this, though.
,
I do not have any proof of this, though.
return
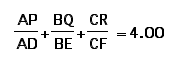 ,
I do not have any proof of this, though.
,
I do not have any proof of this, though.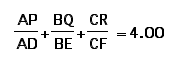 ,
I do not have any proof of this, though.
,
I do not have any proof of this, though.