Final Assignment

 

I construct a GSP file to investigate that triangle.

I found the fact that

.

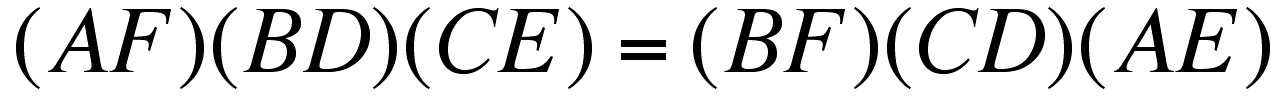This is my conjecture.

you can click here to open the file.

I comstruct parallel lines that are all go through the point P.

In the picture below, GH and BC are parallel, IJ and CA are parallel, and KL and AB are parallel.

Here is my proof to the conjecture.

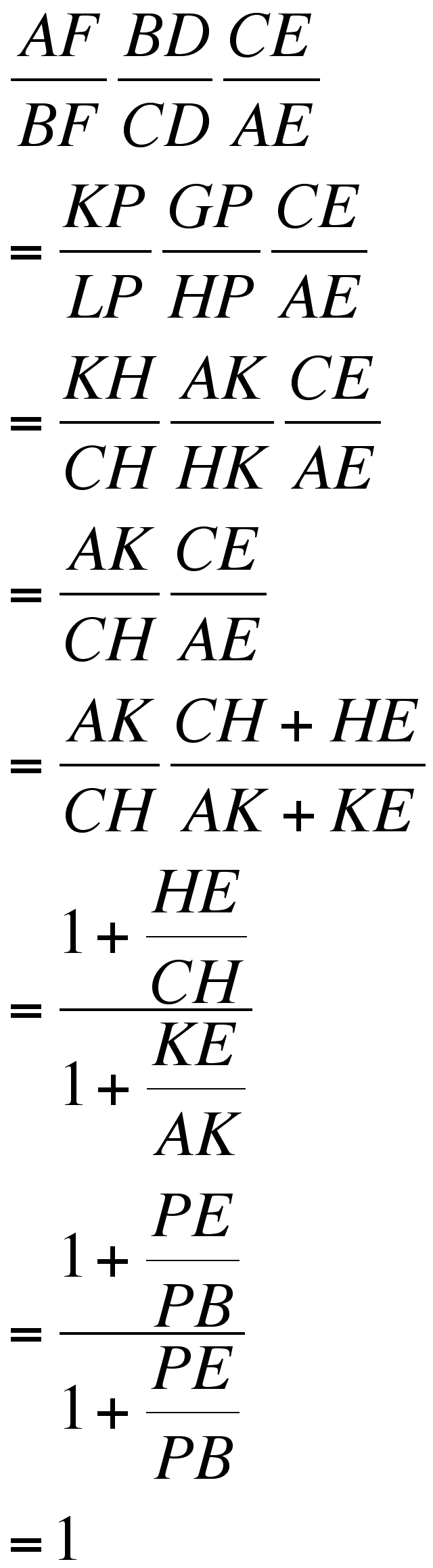So,

.

Finally,

.

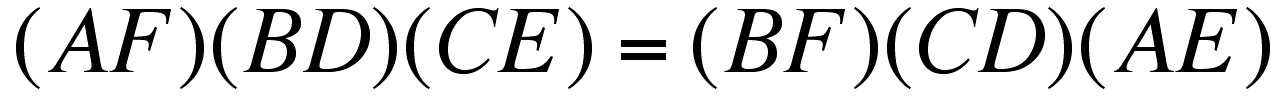This result agrees with my conjecture.

I mesure the area for ABC and DEF

It is when the point P is on the Centroid that the ratio of the areas of triangle ABC and triangle DEF should be 4.

Click here to see the GSP file to check this fact (you can also see that the ratio is always greater than or equal to 4).

I have tried other triangle centers, Circumcenter, Incenter, and Orthocenter, but they are not the case that P is on the point that makes always the ratio 4.

 

It is very easy to prove the fact that when P is the Centroid the ratio of two triangles ABC and DEF is 4.

In the case that P is the Centoroid, DE and AB are parallel, EF and C are parallel, and FD and CA are parallel.

Then, the four triangle, AFE, BDF, CED, and DEF have the same area.

That is why the ratio of two triangles ABC and DEF is 4.

 

return
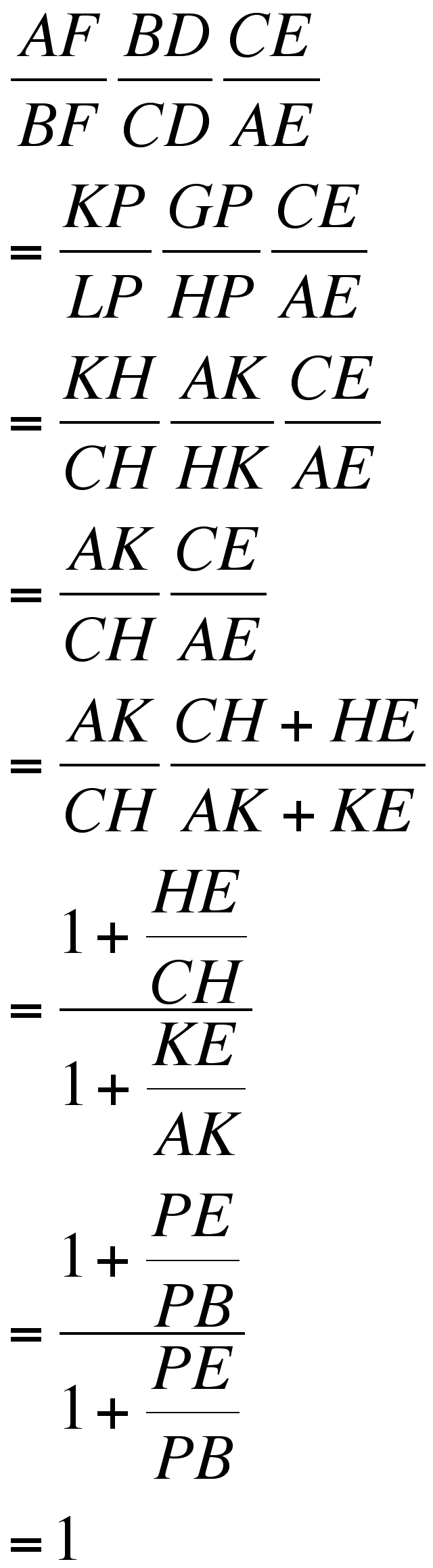