EMAT 6690
YAMAGUCHI, Jun-ichi
In the sprign semester 2005, I take the mathematics course named "Graph Theory(MATH6690)." This course is hard but very interesting and open my eyes to new mathematical world.
I have loved study Graph theory and really want you to study this very young mathematics.
This field of mathematics can be applied for many issues, rainging from operational research and chemistry to genetics and linguistics, and from electrical engineering and geography to sociology and architecture.
What is Graph Theory?
Graph theory concerns the relationship among lines and points.
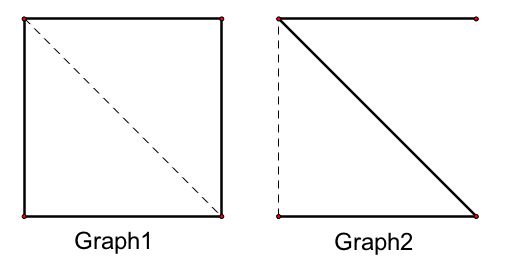
A graph consists of some points and some lines between them.
No attention is paid to the position of points and the length of the lines.
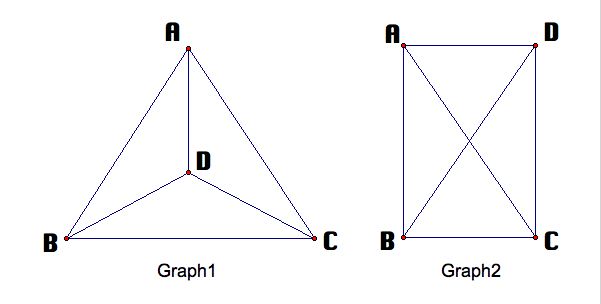
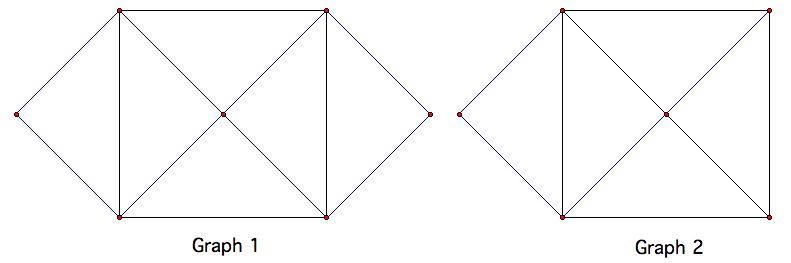
Thus, the two graphs below are the same graph.

You can get more detailed information of graph theory at this site (http://www.netipedia.com/index.php/Graph_theory)
Basic Terms of Graph Theory
a SIMPLE graph G is one satisfying that;
(1)having at most one edge (line) between any two vertices (points) and,
(2)not having an edge coming back to the original vertex.
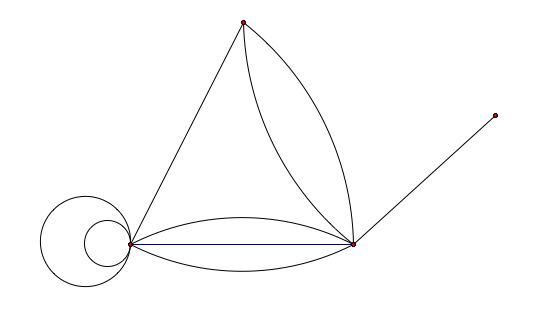
I show two examples of graphs that are not simple.
Example:This graph is not simple because it has an edge not satisfying (2).
The edge is a loop.
Example: This graph is not simple because it has 2 edges between the vertices A and B.

Two vertices, v and w, of a graph are ADJACENT if there is an edge, vx, joining theem; the vertices are then considered INCIDENT to the edge, vx.
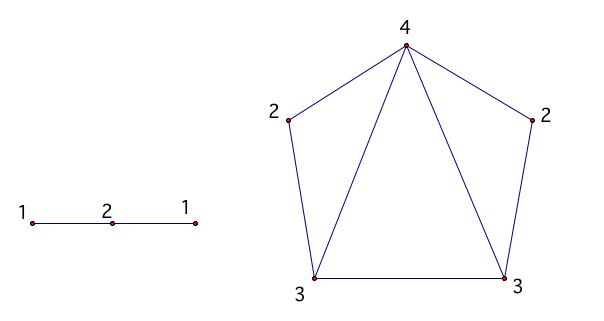
The DEGREE of a vertex v of a graph is the number of edges incident with v.
Eample: The degree of each vertex in this graph below is represented by the number.
Exact definitions on the web page, Math World
Simple Graph (http://mathworld.wolfram.com/SimpleGraph.html)
Vertex Degree (http://mathworld.wolfram.com/VertexDegree.html)
Excercise 1
Find alll of the six simple graphs with 4 vertices.
Excercise 2
Find the dgree of each vertex of the graph below.
Some Interesting Issues in Graph Theory.
I show three issues in Graph Theory that are interesting and basic.
1. Handshaking Lemma (due essentially to Leonhard Euler in 1736)
If several people shake hands, then what is the total number of hands shaken?
(Note that it is not the number of handshakes.)
When we use some terms of graph theory to think of this question, we can consider a vertex and an edge as a person and a handshake respectively.
Since one edge is incident with 2 vertices (note that G is simple), we can easily see that 1 handshake consists of 2 people, that is, 2 hands.

This follows that the total number of hands shaken is twice the number of handsake.
Unfortunately, we can not tell the exact number of hands shaken because we do not know the number of handshakings.
All that we know is that the number is of hands shaken is even.
In terms of graph theory, in any graph the sum of all the vertex-degrees is an even number - in fact, twice the number of edges.
Additionally, we can tell that in any graph the number of odd degree vertices is even.
2. Eulerian graphs
Consider a typical problem of asking whether a given diagram can be drawn without lifting one's pencil from the paper and without repeating any lines(: drawing a picture with a single stroke).
Problem: Which of the graphs 1, 2, and 3 below can be drawn with a single stroke?
aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
Answer:
The graphs 1 and 2 can be drawn in the desired way, but the graph 3 can not.
Did you see the difference between the way of drawing the graph 1 and that of the graph 2?
With regards to the one-stroke drawings of the graph 1, the ending point is the same as the starting point. In contrast, the one-stroke drawings of the graph 2 have a different start and finish.
Like the graph 1 above, if a graph has way of getting from one vertex to another that includes every edge exactly once and ends at the initial vertex, then the graph is Eulerian (is a Eulerian graph).
Like the graph 2 above, if a graph has ways of getting from one vertex to another that include every edge exactly once and ends at another vertex than the starting one, then the graph is semi-Eulerian (is a semi-Eulerian graph).
The name 'Eulerian' arises from the fact that the mathematician Euler was the first person to solve the famous problem "Königsberg bridges problem", which tells you how to cross each of the seven bridges in the Figure below exactly once and return to your starding point.
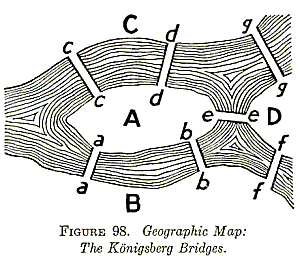
A view of Königsberg as it was in Euler's day
This is equivalent to asking whether the graph below has a Eulerian trail, that is whether the graph is Eulerian.


Exercise: Try to find a Eulerian trail on the Königsberg graph.
Did you try it?
I guess you could not find any Eulerian trail because Euler proved mathematically that no one can find any one-stroke drawing on that graph.
Here is the most famous and simplest theorem (Euler 1736) about whether a given graph is Eulerian or not.
A connected graph G is Eulerian if and only if the degree of each vertex of G is even
By this theorem, the graph of Königsberg bridges problem is unsolovable.
3. Hamiltonian graphs
While we considered in the "Eulerian graph" section a way of going and returning including every edge of a graph, we consider here a similar problem of going around on a graph including every "vertex" (not "edge").
Problem: Which of the graphs 1, 2, and 3 below have a way of passing every vertex?

aaaaaaaaaaaaaaaaaa
Answer:
The graph 1 and graph 2 has such a way (as shown below), but the graph 3 not.
Similar to the story of Eulerian graph, there is a difference between the way of graph1 and graph 2. That is about the ending points of the paths.
With regard to the path of the graph 1, the ending point is the same as the starting point. In contrast, the path of the graph 2 has a different start and finish.
Like the graph 1 above, if a graph has a path that includes every vertex exactly once, while ending at the initial vertex, the graph is Hamiltonian (is a Hamiltonian graph). That path is called a "Hamiltonian cycle".
Like the graph 2 above, if a graph has a path that includes every vertex exactly once, but ending at another vertex than the starting one, then the graph is semi-Hamiltonian (is a semi-Hamiltonian graph).
Recall that in the previous section of "Eulerian" we saw the very simple and useful theorem about telling whether a graph is Eulerian or not. Because, unfortunately, little is known in general about Hamiltonian cycle, the finding of such a characterization is one of the unsolved problems of graph theory.
Problem:
Find a Hamiltonian cycle of the graph below.
One of the answers of this problem
Problem:
Find a Hamiltonian cycle of the graph below.
(This problem is quite hard.However, this does not mean there is no answer.)

One of the answers of this problem
I have introduced some basic terminologies and concepts of graph theory.
I almost end up my explanation for introducing graph theory.
But I have many other interesteing issues I wanted to show.
Here I just make a list of those issues with hyperlinks to the definition and explanation of them.
Some of the issues have strong connection to other study fields.
Issues
|
Area where the issue applied
|
| Tree | Chemistry, Electrical networks |
| Directed graphs (Digraphs) | Comunication theory, City construction planning |
| Platonic graph | Polyhedron |
| Planar graph | Electrical Engineering, Map coloring (Four coloring theorem) |
In my Graph Theory course, I read the textbook "Introduction to Graph Theory, 4th edition"(Robin J. Wilson)
Go ahead and read it to study Graph Theory. I reffered to the explanation of this book in order to make this essay.