

Variables theta, the angle of rotation, and r, the distance a point is from the origin. If we plotted the polar equation r=1, we could see all points that are a distance of 1 unit from the origin (or a unit circle). The radius (or 'r') can also be a function of theta such as the polar equation and graph below.
Let's check out what happens when 'r' is some multiple of theta (for example r=7*theta)
So we want to look at the following polar equation
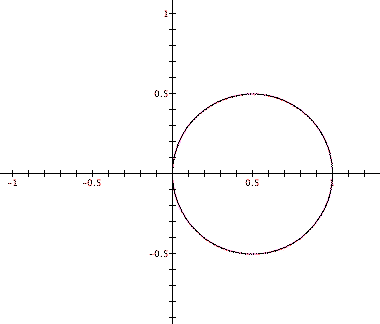
where a is any real number. Select different values for 'a' in this Graphing Calculator file and see what this polar equation graphs. Below is the graph of our polar equation when a=0.1 and theta ranges from 0 to 2pi. How would you describe this graph?
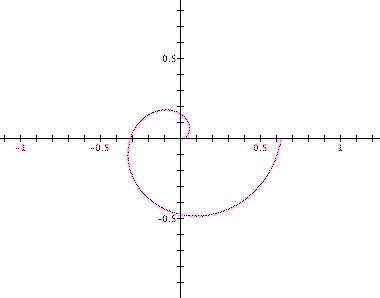
So we see a sort of curly-cue shape. What do you think will happen if we trace more revolutions of our polar equation by increasing the range of theta to, say, 14pi?
Check it out below (notice that the axes of this graph are different than the previous one).
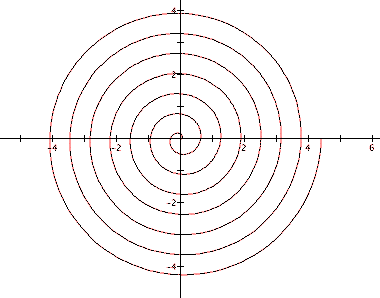
Whoa . . . a little bit more interesting than our first look at our polar equation. At first glance this graph might look like concentric circles, but upon close inspection we see that it is actually a spiral. And not just any spiral . . . the distance between consecutive intersection points of the spiral and either of the axes seems constant. In fact, for every value of theta, the distance between a point at one revolution and the point at the next revolution seems constant. How can we be sure about this conjecture?
First we'll need list the radii for an arbitrary a and theta. So we see that the following is true:
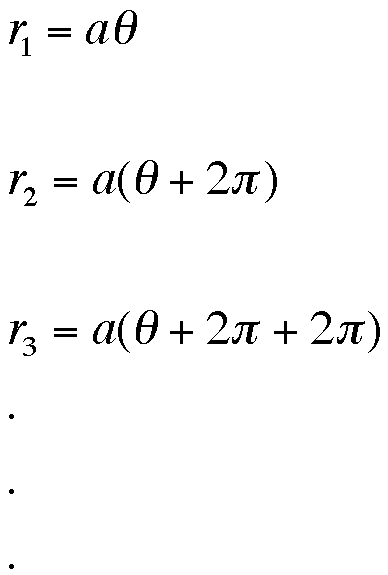
From this we can write a general formula for the radius at any revolution.
Using this general formula, we can calculate the radius at the n+1 revolution.
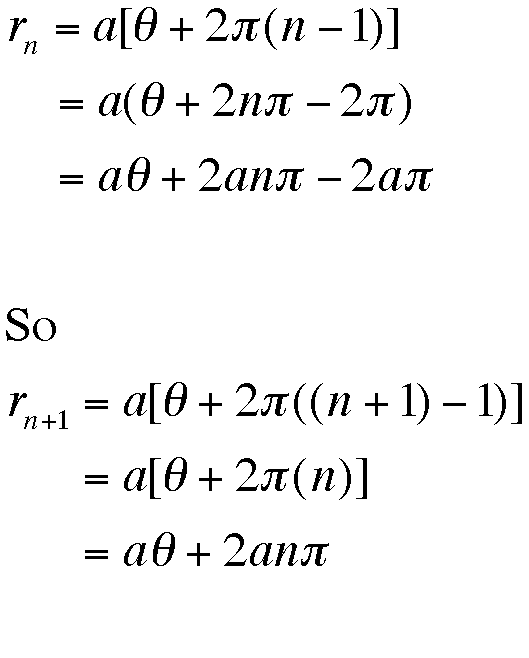
Then all we have to do is subtract these two r values to find the difference between them.
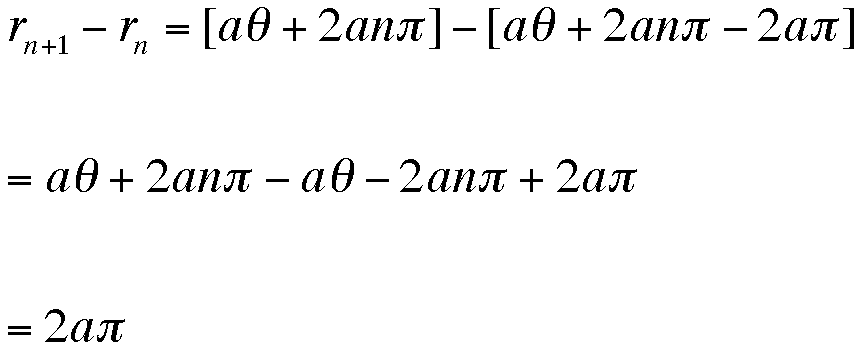
Since 'a' is a fixed value, we find that this distance is constant. And since our theta value was arbitrary, this is true for every theta. This spiral is known as Archimedes spiral. What objects can you think of that exhibit an Archimedes spiral?
So instead multiplying some number by theta, we are going to see what happens when we divide that number by theta, like this . . .
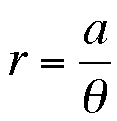
To see a graph of our function we'll need to pick a particular value for 'a', perhaps a=1. So our equation becomes
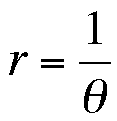
Check out the graph of our equation as theta ranges between 0 and 2pi.
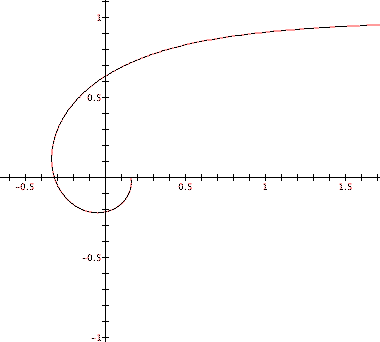
Yet another curly graph. Recall that the Archimedes Spiral curled outward as theta increased. Do you think that this graph is curling outward or inward at theta increases? Why?
To check, let's increase the upper bound of theta (let theta range from 0 to 8pi). Compare this graph below to the first graph of our polar equation.
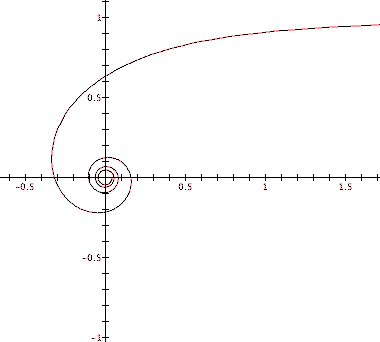
The graph of our polar equation seems to be spiraling inward. Does this make sense with what we know about fractions? Let's look back at our equation.
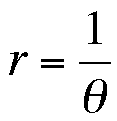
As theta increases, the deonmenator of our fraction gets larger. This means that the fraction is, in fact, getting smaller. Since our radius is equal to that fraction we see that as theta gets larger, the radius gets smaller - that is they are inversely related. So this inward spiraling does make sense.
Now let's zoom our and see what the graph of our equation looks like when theta is very small.
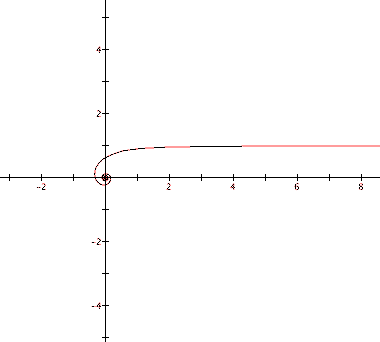
The graph of this equation seems to start out somewhat flat (when theta is small and our radius is very large) and then curl inward rapidly.
PROOF???
Use this Graphing Calculator file to change the value of 'a'. How does this change the graph of the polar equation?
So we find that multiplying a number by theta and dividing a number by theta produce very different polar graphs. Both form spirals, but the properties of each of these spirals are quite different.