The task: To create the lidless box with maximum volume by removing a square from each corner of a 5-inch by 8-inch sheet of paper.
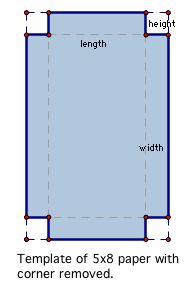
Click on the animation button in this GSP file to look at how the volume of the box changes as the side length of the square removed changes. What is the longest possible side of the square removed? At what side length does the volume seem to be maximized?
To get a sense of how the box's volume varies with the size of the corner piece removed, let's start by looking at some data. Below is a chart showing the side length of the piece removed and the resulting box length, width, height, and volume. Does the relationship seem linear (steadily increasing or decreasing)? Or do things seem a bit more complex?
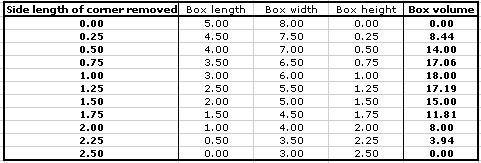
From these data we see a maximum volume of 18.00in^3 when a square with side length of 1 inch is removed from each corner. Hmmm . . . since our data are discrete (that is, not continuous) how do we know that removing a 1-inch square results in a box with the maximum volume ? Perhaps removing 1.1-in squares create a box with greater volume. Let's zoom in a bit to see the volumes of boxes with side lengths near 1 inch.
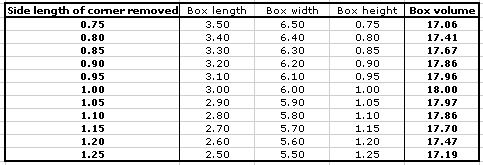
Well, our theory that the greatest volume possible occurs when you remove a 1 inch square is supported. But, we again run into the problem of our data being discrete - we just can't see what's happening between 0.95 and 1.05 and there is always a chance that boxes having a volume greater than 18.0in^3 happen when the squares have a side length between this range.
So, it seems like we need a continuous (and not discrete) picture of how volume is changing with side length. To find this picture, we'll turn the functions. Basically we want to find function that describes the volume of the lidless box for any side length of the square corner removed. Since the volume is the product of the lenght, width, and height all we need to do is figure out how to describe each of these in terms of the side length of the removed square. Let's look back at our template to figure this out.
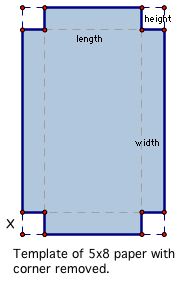
Side length of square removed: Since this is what we'll vary, let's call the side length 'X'
Length of the Box: From the template we can see that the length of the box is related to the 5-inch side of the piece of paper. In fact, the length seems to equal 5 inches minus two side lengths, or 5-2X.
Width of the Box: From the figure we see that the width of the box is related to the 8-inch side of the paper. Much like before, the width is 8 inches minus two side lengths, or 8-2X.
Height of the Box: If we imagine folding the template to form a lidless box, we see that the height of the box is precisely the side length of the square removed, or X.
Volume of the Box: Using the knowledge that Volume = Length*Width*Height we find that the volume of a box is the following:
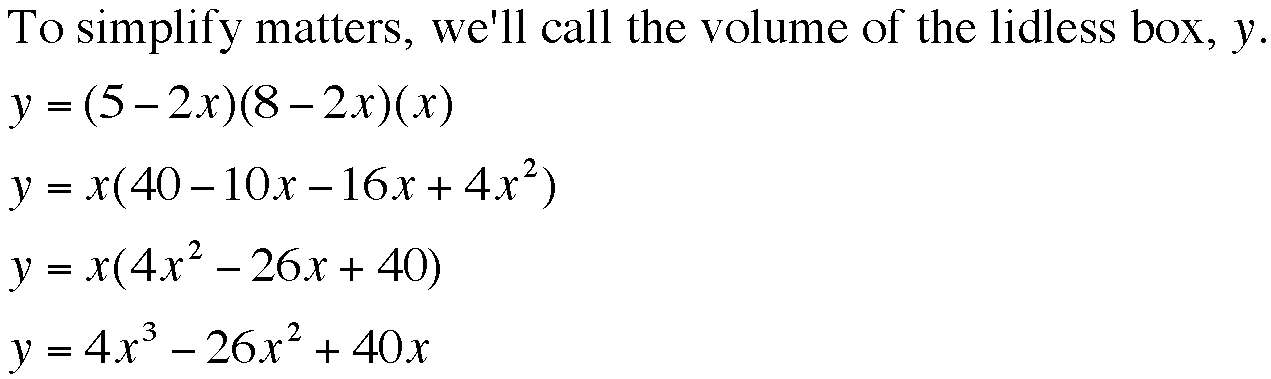
So, we've found a function to describe how the volume of a lidless box varies with the side length of a square removed frome each corner. Let's take a look at a graph of this function.
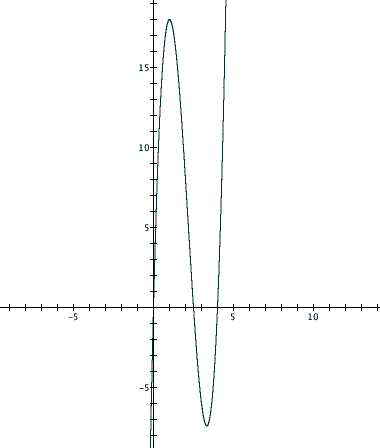
Now we can see the cubic function that describes
our problem. But a question remains, are we looking at the entire
domain of this function, that is can we remove any side length,
'X', that is a real number? In our problem situation, the smallest
length of side removed is 0 inches and the largest side length
of the square removed is 2.5 inches (since the length of the box
is 5-2X, any X greater than 2.5 will create a negative length).
So in reality, we should only examine the portion of the graph
where 
. Within this domain, we can clearly
see that a maximum volume exists somewhere around X=1. You can
click the 'Animate' button in this GSP file
to see how both the volume graph and the shape of our box change
as the side length 'X' changes.
To really find the exact side length where the volume of the lidless box is maximized, we turn to some calculus. Remember that when a function has a local maximum or minimum the derivative of the function at that point is 0 (or, the slope of the tangent line at the maximum/minimum is 0). So, to find our max, we just need to find the derivative of our function and solve for X when that derivative is 0. Here goes . . .
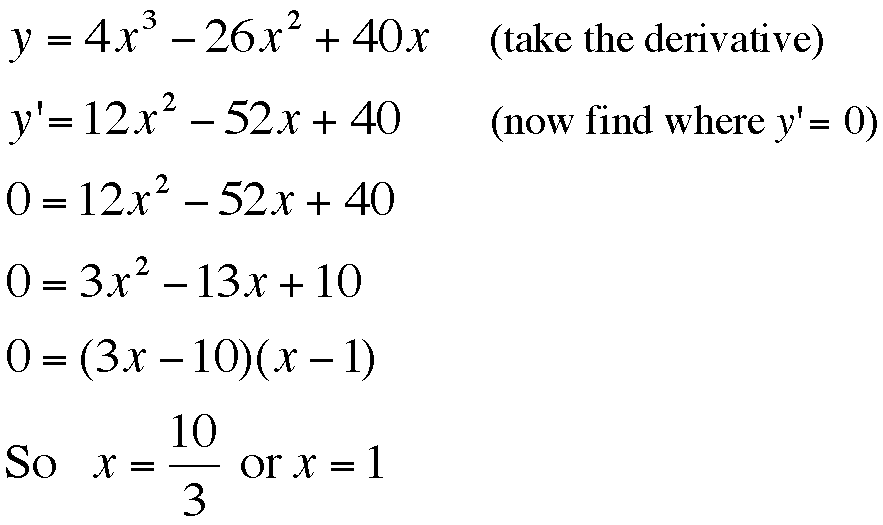
Now if we take a moment to reflect on our solutions
for X, we see that 10/3 is outside of our domain (10/3>2.5).
Therefore x=1 is the only solution for where our volume function
reaches a maximum for 
. Tah Dah! Our hypothesis
that removing squares with side length of 1 inch result in a maximum
volume (18.00 inches cubed) is confirmed.
Well, we've looked our box's volume. What about it's surface area . . .?