So we've looked a little bit at quadratic functions and how changing the coefficients (a, b) and the constant term, c, in the following function changes the graph of the function.
Now let's look more closely at how changing the coefficient of the linear term (that's 'b' in our example above) affects the roots of that function. Recall that a root is the x value where y=0 (often talked about as points where the graph of the function crosses the x-axis).
To do this we'll need to fix 'a' and 'c', that is to say we'll pick some value for 'a' and some value for 'c.' Then we can change 'b' and see what happens. So how about letting a=1 and c=1. Therefore we end up with the following:
Previously we graphed this function and watched how the graph changed when we let 'b' change. Check out the movie below to see how the graph of our function changes as 'b' ranges from -5 to 5. You can also check out this Graphing Calculator file to see more information about the value of 'b' and the corresponding graph.
How would you describe how the graph of our function changes as the value of 'b' changes? What about the roots of the function for different values of 'b.' Do all choices for 'b' create parabolas with the same number of roots? Are there ever situations where the function seems to have no roots? Hmmm . . .
So, if we're interested in roots we're really looking at situations when y=0, that is when the following statement is true:
In the same way that we examine the graph of functions of x and y on the xy coordinate plane, we can look at the statement above on an xb plane. This means that the horizontal axis would represent possible values for x and the vertical axis would represent possible values for b (not 'y' as is usually the case). Take a look below at a graph of our statement in the xb plane.
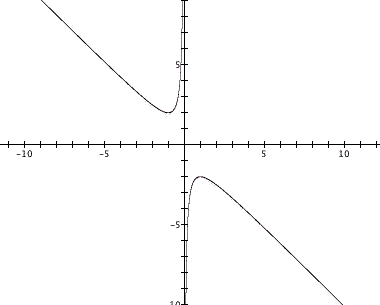
So what does this graph show us? This is actually the graph of all pairs of 'x' and 'b' that make the statement
true - and these pairs are plotted on our xb plane.
Now let's examine our statement for one particular value of b, say b=4. To see this graphically, we'll simply plot the line b=4 on the xb plane (this is the red horizontal line passing through b=4).
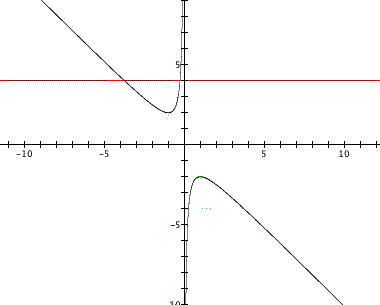
We can see that the line b=4 crosses the function
twice. This means that there are two
values of 'x' which, when we let 'b' be 4 make our statement true.
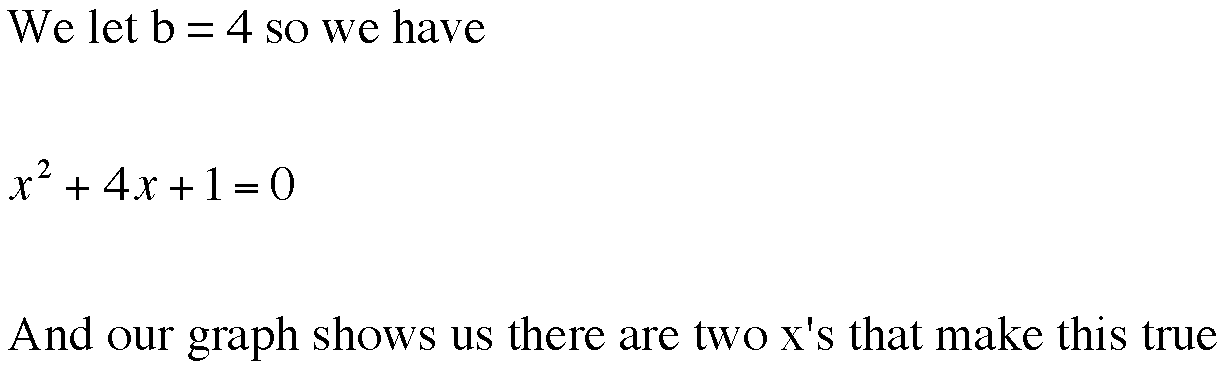
And that's the same as saying the function
has two real roots!
Let's do some algebra to check this.
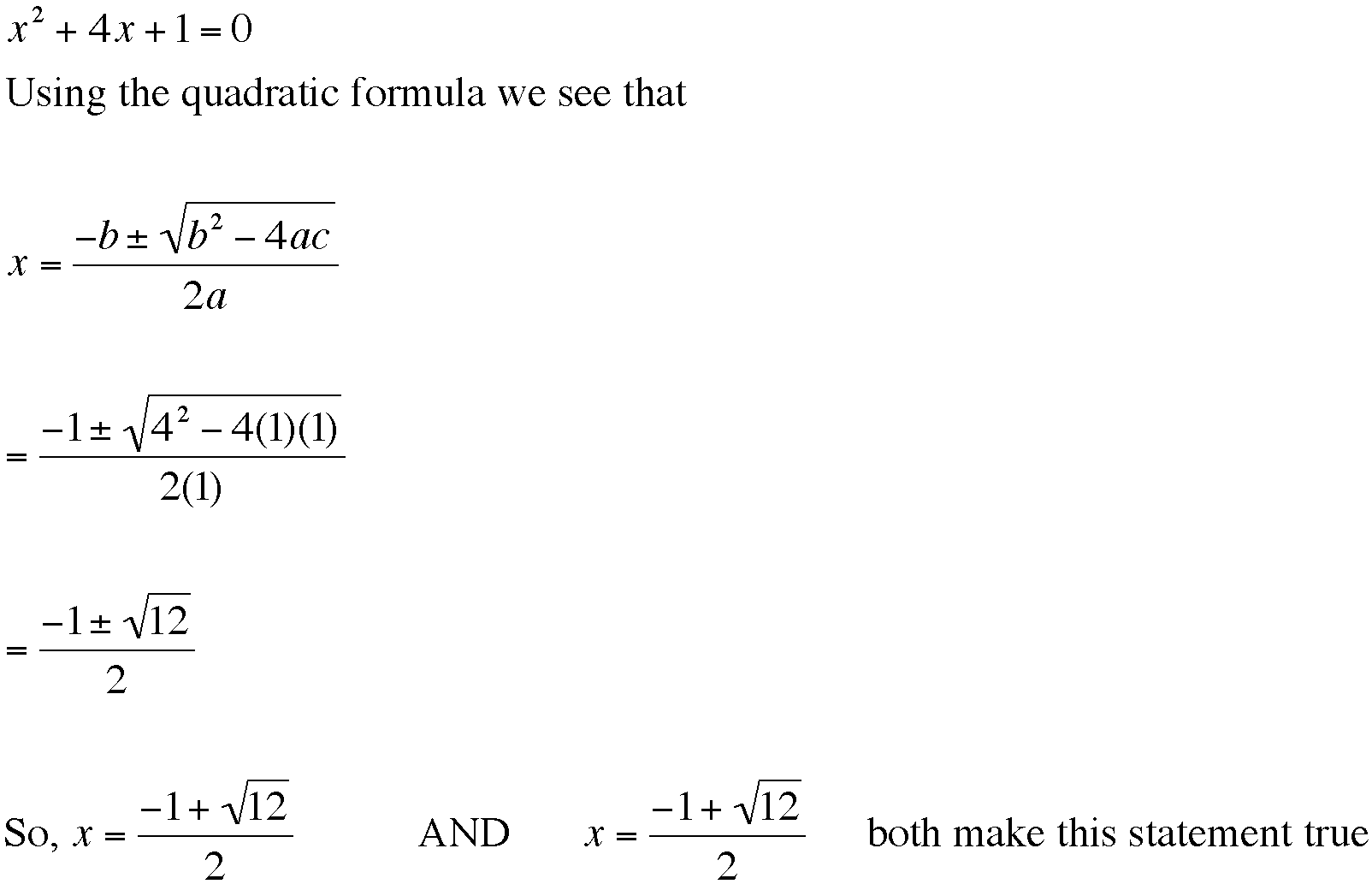
Indeed we have two roots.
So we've see that our graph reveals that there
are two real roots of 
when we let b=4.
Below is the graph of our statement in the xb-plane and some lines
representing various values of 'b'. Does every value of 'b' produce
a function (
)with 2 roots? Are there some cases
where there are no roots?
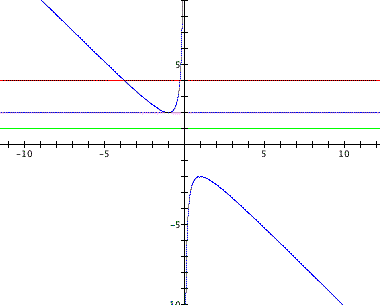
It does look like some values of 'b' don't
have any corresponding x's that make the statement 
true.
In fact this seems to be true when -2<b<2. Let's pick some
b in this range, perhaps b=1, and see if our algebra supports
this idea.
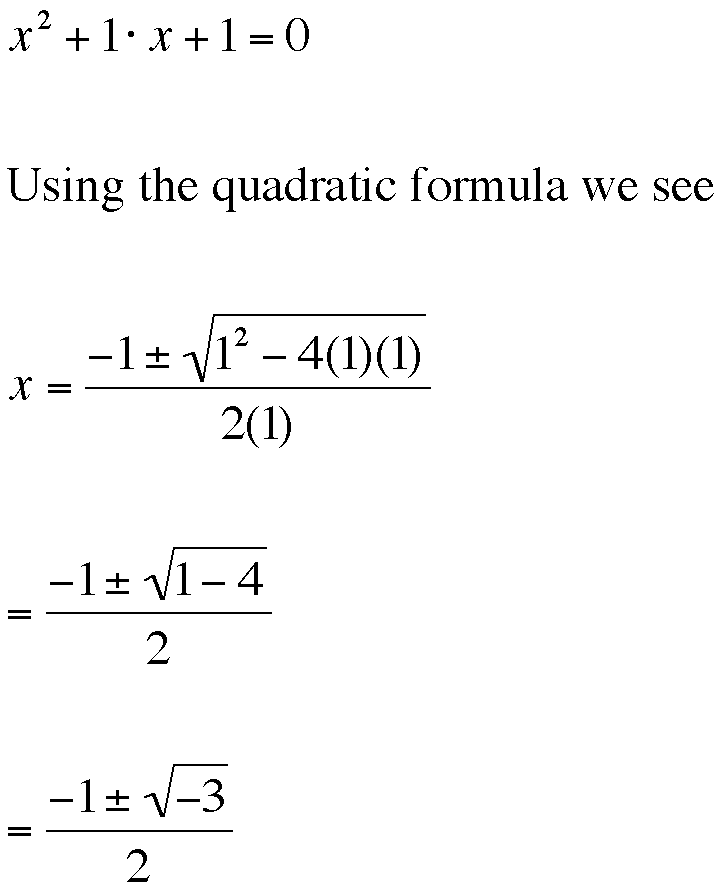
And indeed we have no real roots (only complex ones).
Let's see if our hypothesis that any 'b' between
-2 and 2 results in a function with no real solutions is actually
true. We know real solutions result only when the discriminant
of the quadratic formula (
) is
greater than or equal to zero. So we have
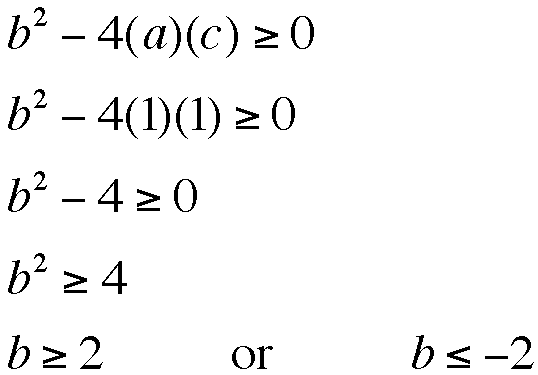
So the hypothesis we made from our graph in the xb plane is supported.
How do you think that our graph in the xb-plane
will change if we let 'c' be negative, for example c=-1. So now
we'd be looking at 
(the roots of 
). Take a look below.
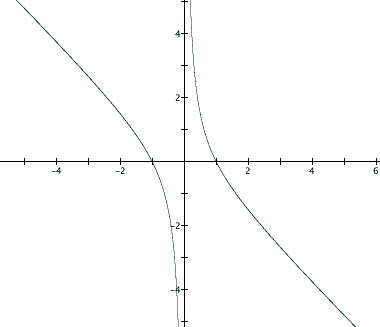
How is this graph different than our previous
graph (
)?
Well, there don't seem to be any values of
'b' for which there are not 2 roots of the function
.
That is to say that any horizontal line we draw (b equals some
number) crosses the graph twice indicating two x-values that make
the statement true. Can we support this observation with some
algebra?
Here goes . . .
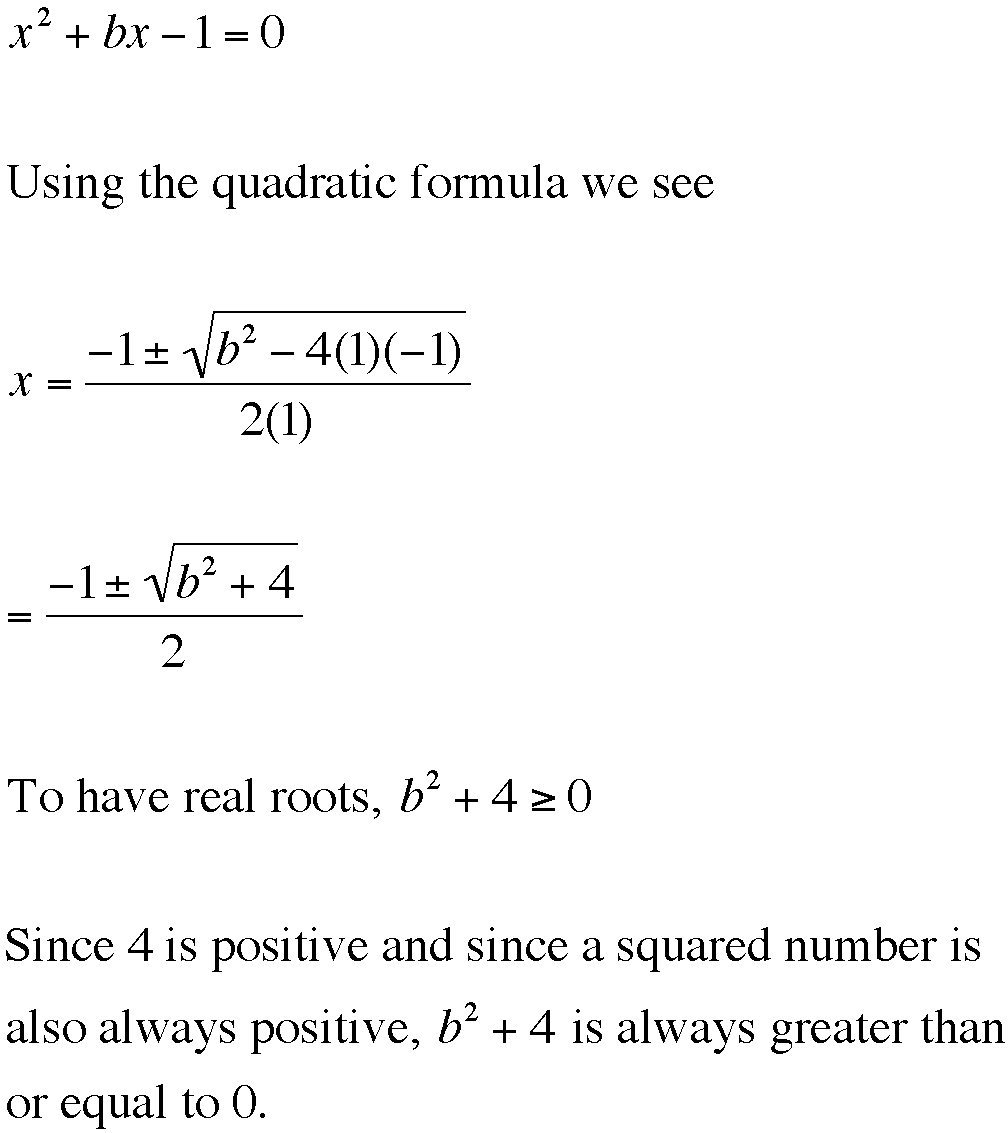
So our hypothesis is true that 
has
2 real roots no matter what the value of 'b' is. Tah Dah!