

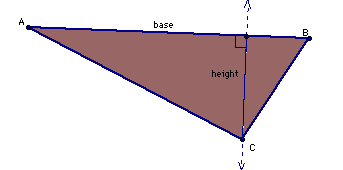
We've heard that the area of a triangle can be calculated by multiplying the length of a base by the height and dividing by two. But what, exactly is a height?
The height, also known as an altitude, has two important properties. First it is a line that passes through the triangle's vertex which is opposite to the base. Second, this line must be perpendicular to the base.
Check out the height of the triangle below.
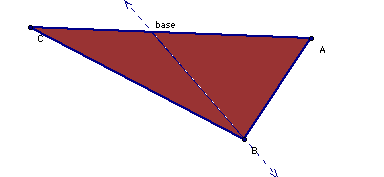
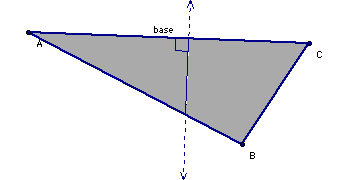
The two triangles below show an attempt at creating an altitude. What is wrong with the "altitude" drawn in each figure?
Not all altitudes are located inside a triangle. Change the shape of this triangle to discover when the height is outside of the triangle. To change the shape of the triangle, click on vertex D (the green point) and drag it around your screen.
Don't be fooled into thinking that triangles have just one altitude. In fact, every triangle has three altitudes, one that is perpendicular to each of the three sides of the triangle.
Altitudes in an Obtuse Triangle
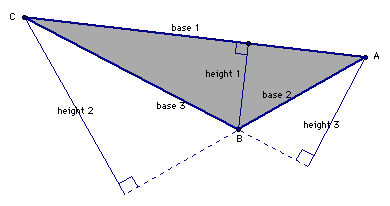
Altitudes in an Acute Triangle
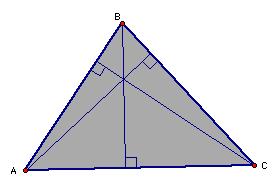
What do you notice about the three altitudes of in the acute triangle? Do you think this is true for the lines containing the altitudes in every triangle? Change this triangle by dragging the vertices and explore whether your hypothesis is true for all types of triangles (acute, right, obtuse, large, small . . .).
Let's prove it!
First we need to situate an arbitrary triangle on the xy plane. Though we could place the triangle anywhere in the plane, it would be most beneficial to put the triangle in the first quadrant with one vertex at the origin and one side resting along the x-axis. Now we can let C be any point on the x-axis, that is (c,0), and B can be any point in the first quadrant, or point (d,e).
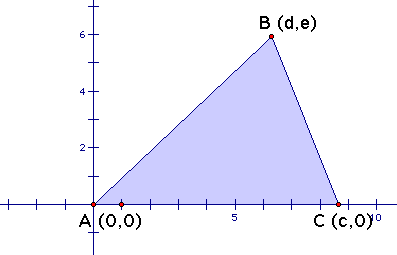
To prove that the perpendicular lines through each vertex (the ones containing the altitudes) intersect at one point, we'll need to find the equation of each line and find one point, (x,y), that satisfies all three equations. The equation of each altitude will have the general form
where 'm' is the slope and 'b' is the y-intercept of the line.
So how do we find the slope of the altitude?
From our construction of the altitude we know that it must be perpendicular to its base. So, this means that the slope of the base and the slope of the altitude are related. In fact, because they are perpendicular they have the following relationship:
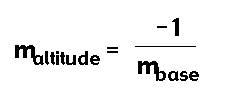
Now all we must do to calculate the slope of the altitude is to find the slope of its base.
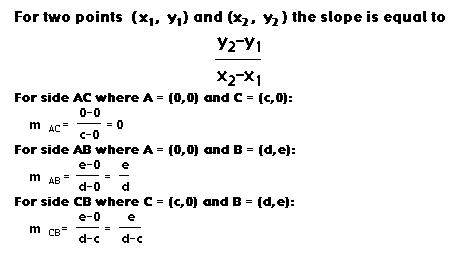
Using our knowledge of slope and perpendicular lines, we calculate the following slopes for our altitudes:

If we can figure out an equation for each altitude line, we can solve the system of equations to see where they intersect (and thus find out if all three lines intersect at one point). So, let's find the equation for each line.


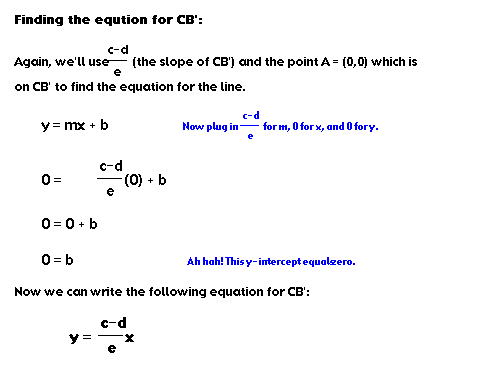
We know, from the equation of AC', that the x-coordinate of the intersection of AC' and AB' must be d. So let's plug d in for x in our equation for the line AB'.
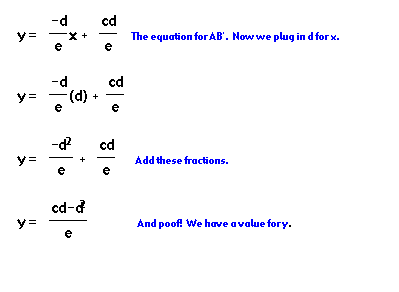
So we've discovered that AC' and AB' intersect at following point:
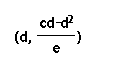
Now the question becomes does this point also lie on BC'. If so, then we discover that this one point is on all three lines containing the altitudes of our triangle and thus they intersect at one point. To see if the point satisfies the equation for BC' we just need to plug in the x and y values for the point into the equation for BC' and make sure the resulting statement is true.

Since this statement is true, our point satisfies all three equations for the lines containing the altitudes of the triangle. That means all three lines pass through our point and must, therefore, intersect at one point, namely
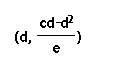
as we suspected!
And since our triangle was arbitrary, this must be true for all triangles.