

So, the burning question exists - What is the locus of points that are equidistant from a circle and a fixed point.
Recall that, as a rule of thumb, distance is measured along a perpendicular line between two objects. Thus, when we examine the distance a point is from a circle, we need to measure along the line perpendicular to the circle that passes through that point.
To find all the points equidistant from our given point, A, and our circle, we should first pick an arbitrary point on our circle (we'll call it P). We need to figure out what point is equidistant from A and P, the arbitrary point on our circle.
We know that the distance from our mystery point to P (on our circle) must be measured along the line passing through P which is perpendicular to our circle. In fact, this perpendicular line is actually the line through CP.
Let's stop for a moment and think ahead to what our picture would look like IF we knew where our mystery point was.
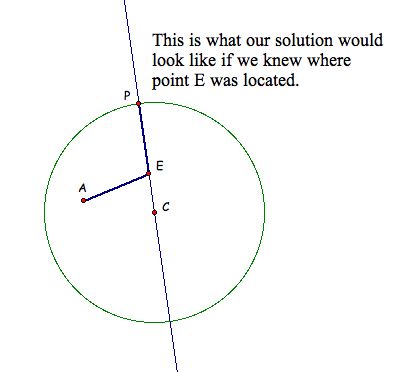
Using our 'solution' picture we can form the triangle AEC - check it out below.
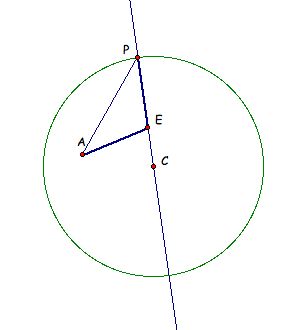
In fact, since the distance from A to E and the distance from E to C are the same (remember, that's what we were trying to construct in the first place!) triangle AEC is actually isosceles. Hmmm . . . what do we know about the vertex of any isosceles triangle? It lies along the perpendicular bisector of the base of the triangle. So this means that point E (the vertex of this particular isosceles triangle) must be on the perpendicular bisector of segment AC.
So let's jump back to where we were in our construction and find out how this new information helps us locate point E.
What do we know so far? (1) Point E must be on the line CE and (2) Point E must lie on the perpendicular bisector of segment AC.
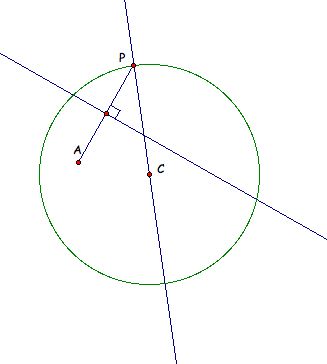
Thus is must be the case that E is the point of intersection of line PC and the perpendicular bisector of AC - Tah Dah!
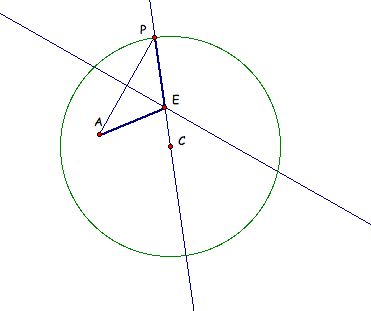
Now that we've found the point equidistant from A and the specific point P on our circle, what is the location of 'E' for all of the points of the circle. To figure this out we can simply move P to all possible location on the circle. In this GSP document click on 'Animate Point' to move P around the circle - the path of E (the point equidistant from A and P) will show up as a red trace. What do you notice about the location of E? Do you see a general shape for all the points equidistant from A and our circle?
So, it seems like the locus of points equidistant from the fixed point A and and our circle form an ellipse having foci A and C. But can we prove it?
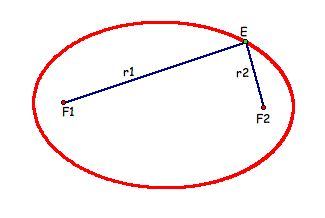
First, let's figure out exactly what an ellipse is. If we look at the picture below, we find that an ellipse is the set of all points E for which the following is true: r1+r2 = c where c is come constant value.
So, in order to prove that the locus of point equidistant from a fixed point and a circle is an ellipse, we need to find our two foci and the make sure the sum of r1 and r2 is, indeed, a constant. Let's look back at our construction.
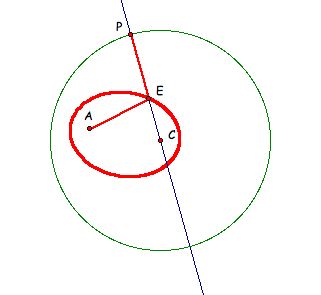
Let E be an arbitrary point equidistant from A and our circle. We see that the candidate foci of the ellipse are A and C and that r1 is the length of AE (we'll call it AE) and r2 is the length of EC (we'll call it EC).
So r1 + r2 = AE + EC
From our construction we know PE (the length of segment PE) equals AC.
Thus AE + EC = PE + EC
Take a look back at our picture. What is PE + EC? Well, segments PE and EC form the radius of the circle, which is constant!
Thus r1 + r2 = c where c is the radius of our circle. Since E was arbitrary, this must be true for every point equidistant from A and our circle. Thus our hypothesis that the locus of points forms an ellipse is supported.
Move point A to different locations in this GSP file (inside the circle, outside the circle) and then animate the point P. The path of A will be traced in red. To erase a trace, simply click on the 'Display' menu and select 'Erase Trace. ' What do you notice? Is the locus of points equidistant from A and the circle always an ellipse?
Let's move point A outside of the circle and use the same construction as before to find the point E which is equidistant from the circle and A.
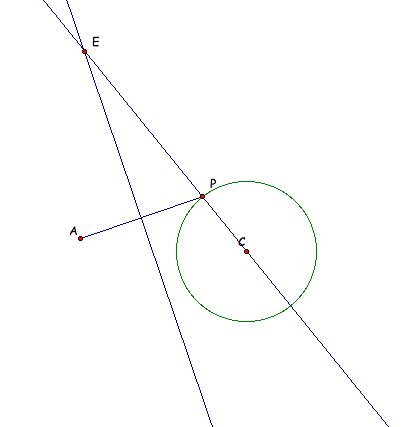
Click on 'Animate' in this GSP file to see how E moves as P goes around the circle. The resulting trace represents the locus of points equidistant from A and the circle. Does this look like the ellipse we saw before? If not, what does the locus of these points resemble?
What's that you say, it looks like a hyperbola? Hmmm . . . how can we be sure? Let's look at the definition of a hyperbola and see if the locus of our points fits that definition. Take a moment to look at the graph of a hyperbola below.
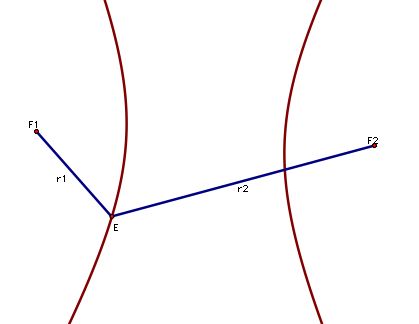
Much like an ellipse, the definition of a hyperbola deals with the location of two foci. However, for a hyperbola the following relationship is true:
r1 - r2 = c where c is a constant.
Let's look back at all of all points equidistant from a fixed point, A, and a circle (when A is outside of the circle).
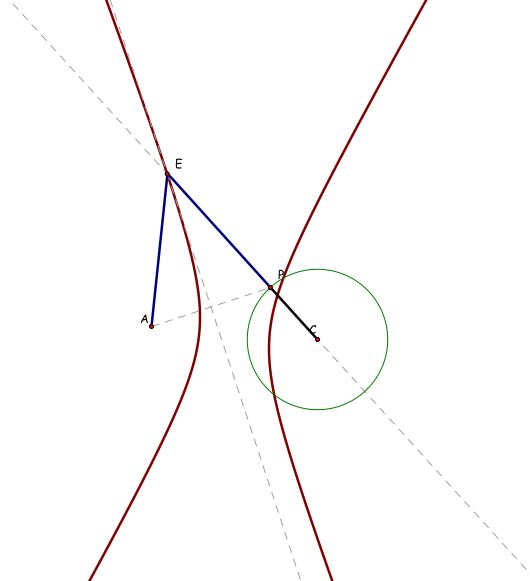
Point A and Point C seem like the potential foci of our 'hyperbola' - let's see if the difference of the distances from each foci to our point E is a constant. We'll denote the length of a segment having endpoints G and H as GH.
We want to examine r1-r2 which is equal to EC-EA. Since EC is composed of the two segments EP and PC, our expression becomes EP + PC - AE. From our construction we know that the length of segment AE is equal to the length of segment EP Thus EP + PC - AE = PC
So r1 - r2 = PC and looking closely we see that PC is the radius of our circle which is, in fact, constant. Thus the locus of points is actually a hyperbola.