

Given 2 circles, one located entirely within the other, and a point on the larger circle we can construct a circle tangent to the large circle at the given point, A, that is also tangent to the small circle. The question is, how do we do this? Basically, all we have to do is find the center of the tangent circle.
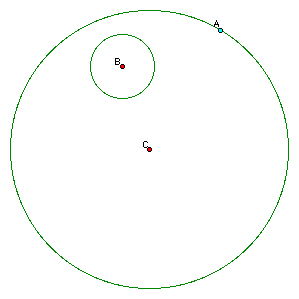
In order for our unknown circle to be tangent at point A, it's radius at A must be perpendicular to the large circle. That is to say that the center of our unknown circle must lie on line CA. Check it out below.
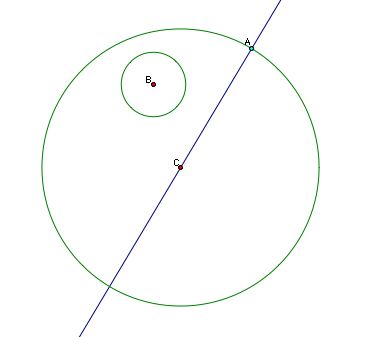
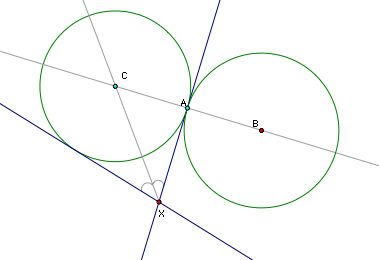
This narrows things down some, but we still don't know where on line AC the center of our tangent circle is located. To figure this out, let's look at an approximate picture of our solution to see if we can get some information about where our center lies.
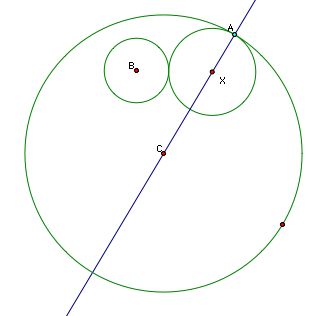
The point of tangency with our mystery circle and the small circle must lie on the segment BX.
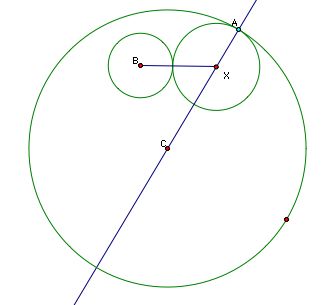
And we see that the distance from B, the center of the small circle to X, the center of the mystery circle is the radius of the small circle plus the radius of the small circle. If we could figure out how to create the base of an isosceles triangle having X as its opposite, we can complete our construction (simply find the perpendicular bisector of the midpoint of that base, and we know X must lie on that line). Let's construct a copy of the small circle with center A - - see below.
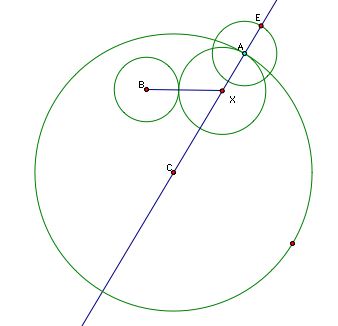
Looking closely at the diagram you can see that the length of segment XE is the same as segment BX (small radius plus mystery radius) - the sides of our isosceles triangle! Using this we can form the base of the isosceles triangle and ultimately find the center, X, of our mystery circle. Let's go back to our picture (without the approximated solution) and follow these steps to construct the center, X. First we need to construct the small circle having a center at A.
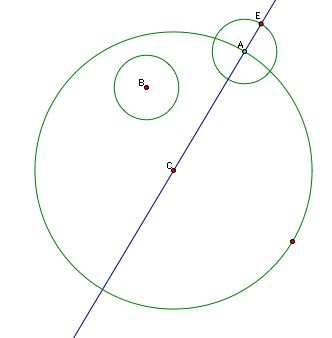
From our analysis of the approximate solution we know that BE forms the base of an isosceles triangle. If we construct this base, and then construct the perpendicular bisector we know X lies on this line.
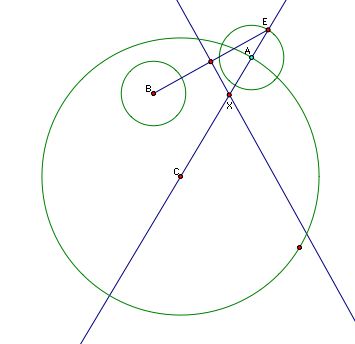
Since we know that X lies on both the perpendicular bisector of BE and the line CE, it must be at their intersection point. Now that we know the center of our mystery point, we can simply use XA as a radius and construct the circle. Tah Dah!
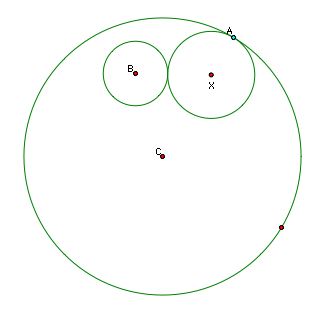
Question: What is the trace of the midpoint of our mystery circle as A moves around the large circle? Use this GSP file to explore.
That is to say, if we're given a line and a circle with point A, how do we construct the circle tangent to the circle at point A and also to the line? Let's take a look at a picture.
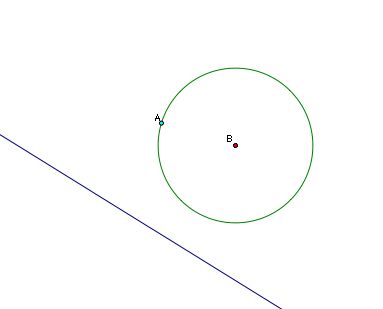
As before we know that the center of a circle tangent to our given circle at point A must lie on the line AB. But we still need to figure out where on line AB the center of this circle sits. Again, let's look at an approximate solution in order to gather information that would help us construct C, the center of our mystery circle.
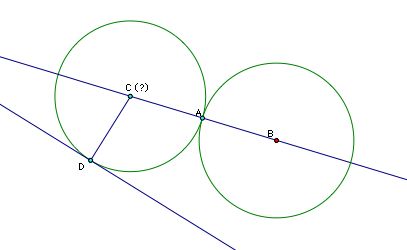
Looking at an approximate solution, we see that the segments CD and CA must be congruent (both are the radius of our mystery circle). We also know that CD is perpendicular to our given line. So if we construct a line through A perpendicular to ine BC, then we create a kite.
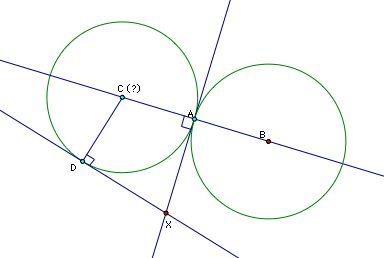
And since quadrilateral CDXA is a kite we know that C lies on the angle bisector of DXA. Let's go back to our original picture and work backwards to construct C.

First we need to construct line AB, then we can construct the line through A perpendicular to AB. The intersection of this line with our given line is one vertex of our kite.
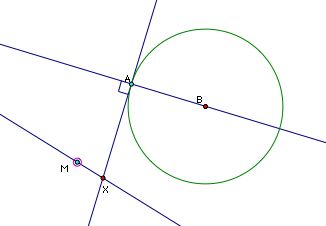
And we know that C, the center of our mysterious tangent circle, lies on the angle bisector of angle AXM (note M is just some point on our given line).
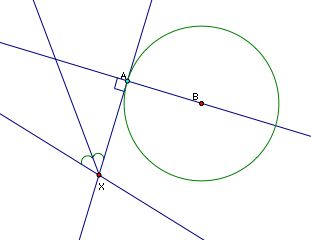
So C must be located at the intersection of the angle bisector and line AB. Using CA as a radius we can now draw the circle tangent to our line and our given circle at point A. Tah Dah!
How would you construct the tangent circle if our given point were on the line and NOT on the circle? Try it out using this Geometer's Sketchpad file.