

In previous investigations, we found that the three altitudes of a triangle intersect at a single point, known as the orthocenter. Let's delve a little deeper into the business of orthocenters.
First we'll take some acute triangle, construct it's orthocenter and also construct the triangle's circumscribed circle. Check it out below.
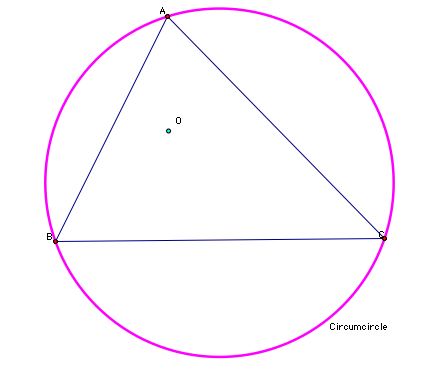
Notice that if extend the altitudes, they intersect the circumcircle. Let's label these points of intersection.
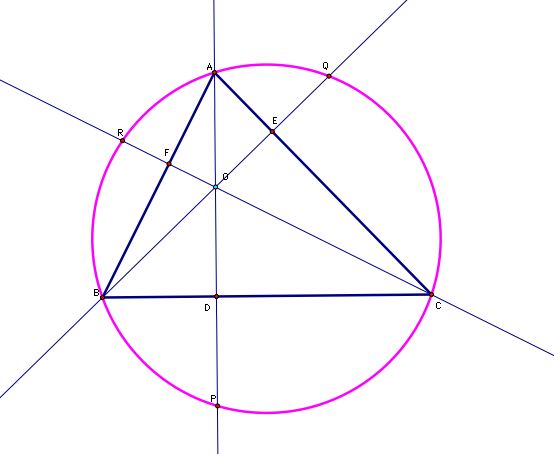
We can form a ratio of the length of the altitude (e.g. AD) and the length of the segment created by extending that altitude across the circumcircle (e.g. AP).
So I wonder if there's anything interesting about the sum of these three ratios?
Use this GSP sketch to investigate. Each ratio and the sum of the ratios is calculated in the sketch. Move the vertices of the triangle around (but make sure it's acute) and see if you find a pattern.
Well it seems like to following is true for every acute triangle we make.
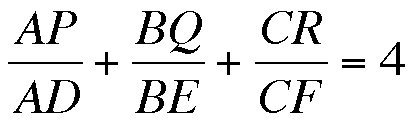
Now, how can we prove that's true?
Since each 'extended' altitude is made up of two smaller line segments, let's start by rewriting the length of the 'extended' altitudes as follows:
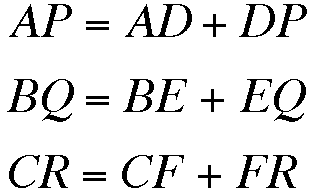
How does this change our sum?
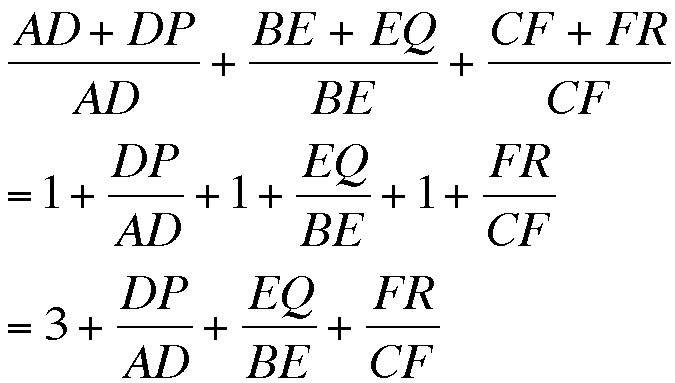
Well, if our hypothesis is true then it must be the case that
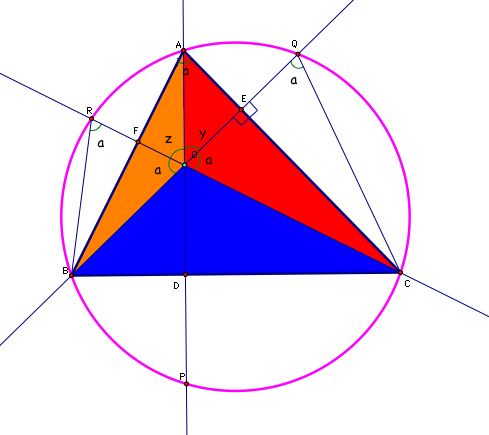
Let's look back at our picture. It sure does look like triangle OEC is congruent to triangle QEC. I wonder if that's true. Well, we can label some angles in our picture.
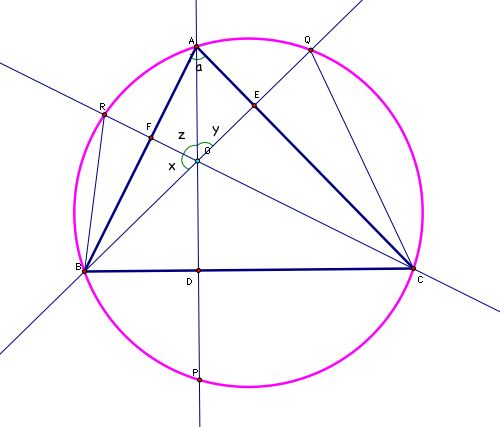
Since triangle AFO is a right triangle, we know that the measure of angle FAO is 90-z. Likewise, the measure of angle EAO is 90-y. Looking at our picture we can see that angle 'a' is composed of angle FAO and angle EAO. Therefore
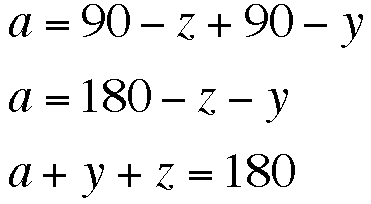
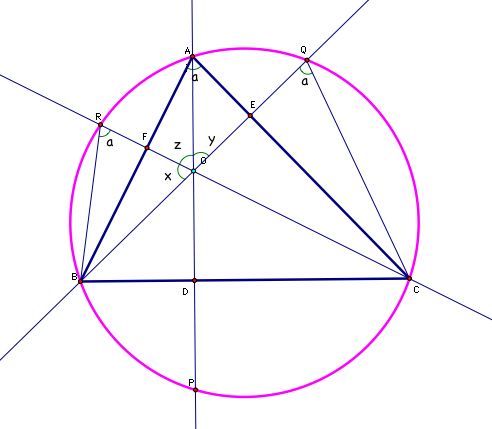
Since angles BRC, BAC, and BQC all subtend the same chord on our circle, they must all have the same degree measure ('a'). So we can fill in our picture as follows
Look along segment BQ around the orthocenter. You can see that the sum of angles BOF, FOA, and AOE must be 180 degrees. So we find that
But we know that a+y+z=180. Therefore the following must be true:
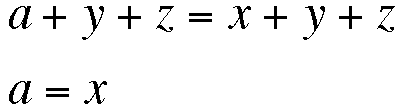
By the vertical angles theorem we know the measure of angle COE must also be 'a'.
So we probably need to look back at the triangles we think are congruent.
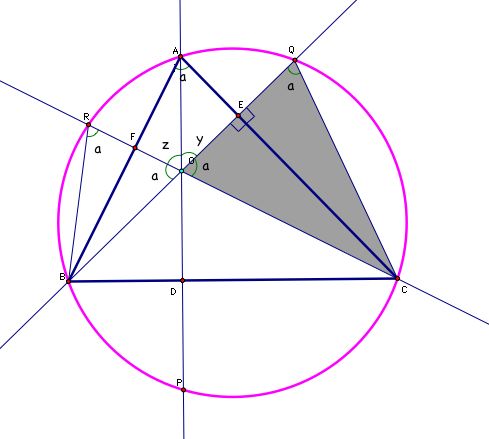
We know they are both right triangles (by construction) and we now know that they both have an angle that measures 'a' degrees. This implies that our two triangles are similar. Hmmm . . . but they share a common side across from angle 'a' (segment EC) and this means that they have to be congruent. Since our two triangles are congruent we know the lengths of segments OE and QE are equal. By similarity we also know RF=OF and OD=OP.
So we can change the sum that we're investigation to
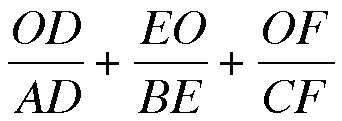
Let's look at the ratio DO/AD. We can multiply this fraction by BC/BC to get the following:
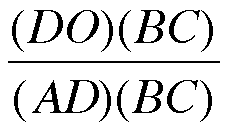
Look back at our picture. We see that since AD is an altitude, BCxAD is actually twice the area of triangle ABC (since A = 1/2bh, BE = b, and AD = h). Similarly, DOxBC is two times the area of triangle BOC (b=BC and h=OD). *We'll deonte the area of any triangle LMN as (LMN)* So now we have
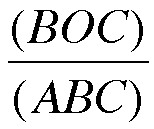
What happens when we do something similar to our other fractions (multiply OE/BE by AC/AC and multiply FR/CF by AB/AB).
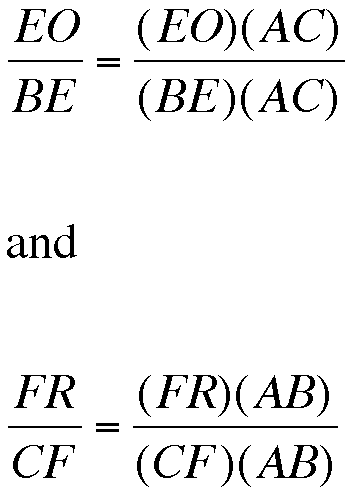
Well, OExAC is twice the area of AOC and FRxAB is twice the area of triangle AOB. Notice the denomenator of each fraction is twice the area of triangle ABC. So our sum has now become
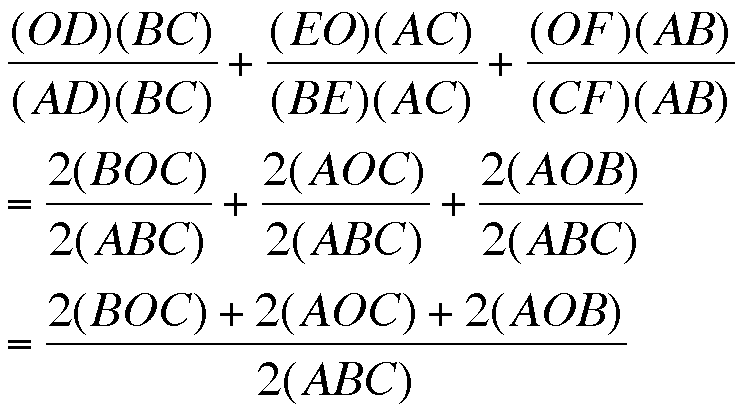
If we add the area of triangles BOC (blue), AOC (red), and AOB (orange) then we have the area of triangle ABC.
So our sum simplifies to
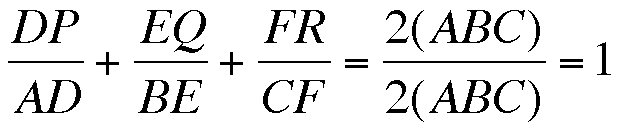
Therefore we find that

Tah Dah!