

Given any triangle and a point, P, we can construct a second triangle known as the Pedal triangle by doing the following:
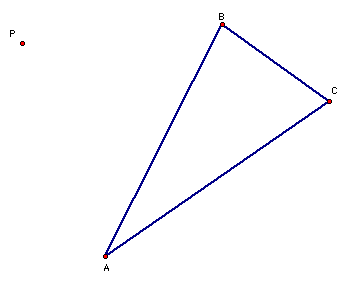
First we want to construct a line through P that is perpendicular to one side of the triangle . To do this we'll need to extend the sides of our triangle.
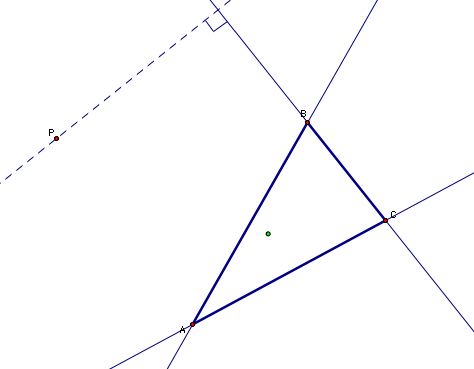
Now repeat this process for sides AB and AC so you have three lines all passing through P which are perpendicular to the sides of the triangle. The intersections of these perpendicular lines with the extended sides of the triangle are the vertices of our Pedal Triangle (N, M, L).
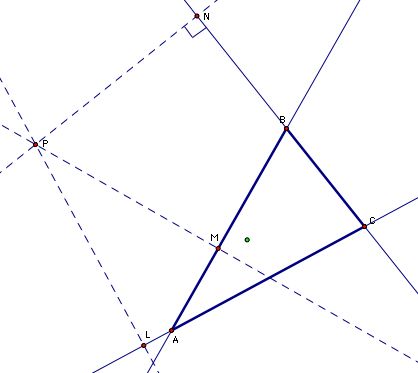
Connecting these three points, we find the Pedal triangle to triangle ABC with respect to point P.
Do you think that the pedal triangle look the same if we change the location of P? Move the pedal point in this GSP file to see if the pedal triangle changes (different locations, shapes, etc)? Can you find a location for P where the pedal triangle is not, in fact, a triangle? Is there more than one location where this is true?
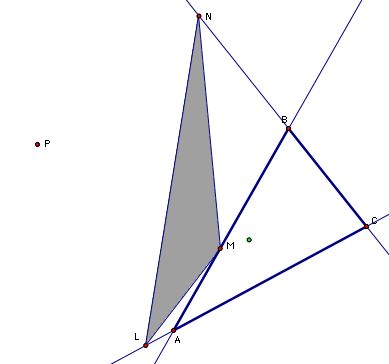
In fact, if P is located anywhere on the circumcircle of triangle ABC, then the Pedal Triangle will actually be a line. This line is known as the Simson line (Segment NL in the picture below). Animate the Pedal Point, P, in this GSP file to see how the Simson line changes as the location of P changes.
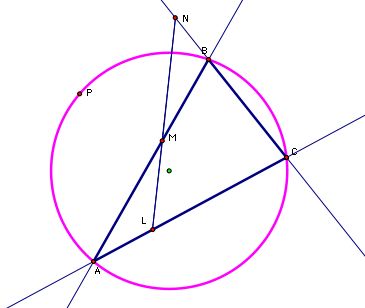
Is there a location for P on the circumcircle so that side AB is the Simson line? Move P in this GSP file and try to find this particular location.
This picture below seems to show a location for P so that the Simson line is on side AB. Now, let's find a way to construct this point for any triangle.
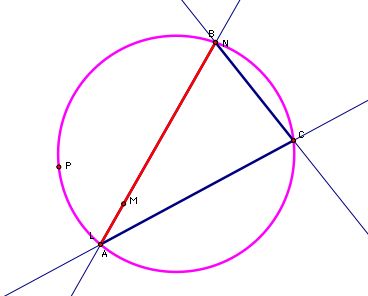
So our goal is to figure out the location of P (our pedal point) so that the pedal triangle is a Simson line equal to AB. First let's back at our original triangle. To create the pedal triangle we need to extend the the sides of our triangle like this.
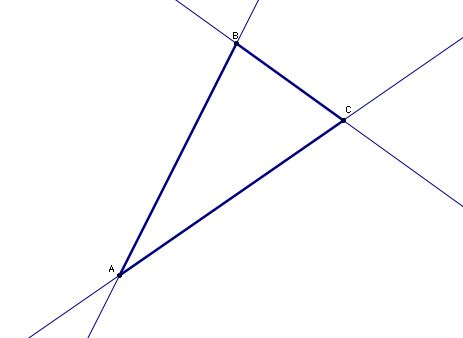
One vertex, N, of the pedal triangle must lie on line BC. If we want our pedal triangle to be a Simson line equal to side AB, then N must also lie on AB. Well, the only point that lies on line BC and AB is point B. Thus the "vertex" of our Simson line must be point B. From the construction of the Simson line, we know that B is found by forming a line perpendicular to BC through P (which is what we're looking for). Working backwards, if we form the line perpendicular to BC through B, we know that P must lie somewhere on this line. Check it out below.
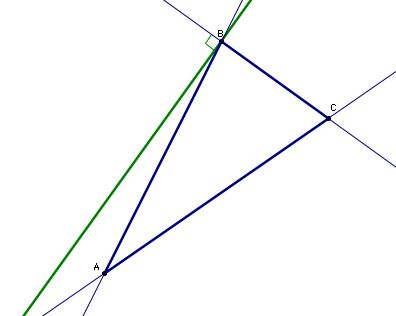
Similarly one point, L, on our Simpson must lie on AC AND also lie on the segment AB. Thus L must be the intersection of these two lines, namely A. Like before, we know that the Pedal point must lie on the line through A perpendicular to line AC. Let's construct this line that we know contains the Pedal point.
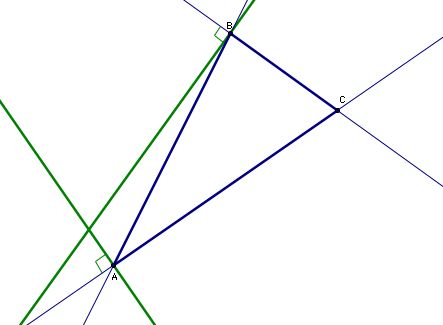
We know that the pedal point must lie on each perpendicular (green line). To do this, the Pedal point must be located on the intersection of our green lines. Ah hah, we've found it!
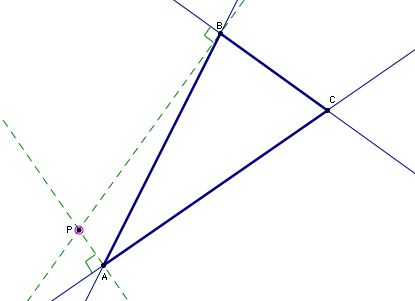
Do you think a Simson line of triangle ABC can equal side BC? What about side AC? How would you find the location of pedal points that create these Simson lines? Try it out using this GSP file.