In attempting to illustrate the process of cell division, many biology textbooks draw a sketch of one large circle (a 2-dimensional version of a cell) with two small 'daughter' cells below it. These daughter cells are shown to have a radius equal to one half of the original cell. A discourse on the mathematical errors inherent in these diagrams can be found here.

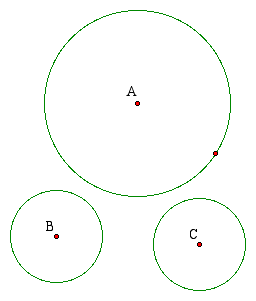
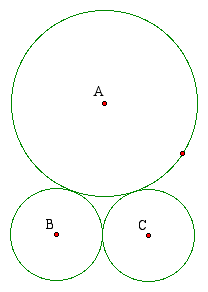
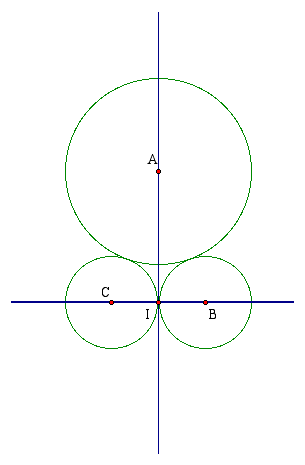
The present task is to construct a diagram of this process such that each daughter circle is tangent to the other daughter circle AND tangent to the large circle. That is, we're hoping to construct something that looks like this . . .

It is useful to begin with a circle and a line through the center of the circle. We will use this line as a foundation of our construction.

The centers of the small circles will lie on a segment perpendicular to the line shown. The problem remains to figure out how far from the center of the large circle this line must be.

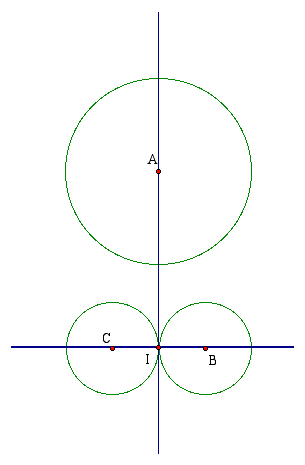
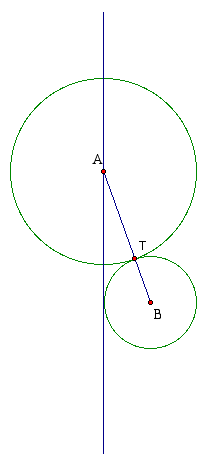
Recall that when two circles are tangent, the point of tangency lies on the line connecting the centers of the circles. For our construction, this means that T, the point of tangency between circle A and B lies on the line AB.

Observing what the final construction would look like, notice that the segment AB is 1.5 times as long as the radius of the large circle (note that the radius of the small circle is half that of the large circle). For simplicity, we'll assume the radius of the large circle is 1, meaning AB is 1.5. Therefore, the center of the small circles must lie on somewhere on the circle centered at A with radius 1.5 times AT.

Additionally, the distance from B to the line through A is 0.5 times the radius of the large circle. Recall that the distance from a point to a line is measured along a perpendicuar line. Thus we are left with the following right triangle:

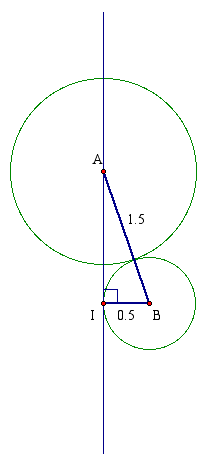
Notice that point I is the exact position where the line containing the centers of the small circles should like. Now, how far is I from A? It looks like time for the Pythagorean theorem. Notice that triangle AIB is a right triangle with hypotenuse of length 1.5 and leg with length 0.5. From the Pythagorean theorem we know that

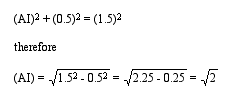
Ah hah! We have a location for point I. Now we need to construct a segment of length so that we can construct a circle through A with a radius of and find I.

To do this we'll build upon our knowledge of isosceles right triangles. If given a right triangle with legs of length 1, the hypoteuse is found to be

So, we simply need to construct an isosceles right triangle with legs having the length of the radius of our large circle. Check it out below.

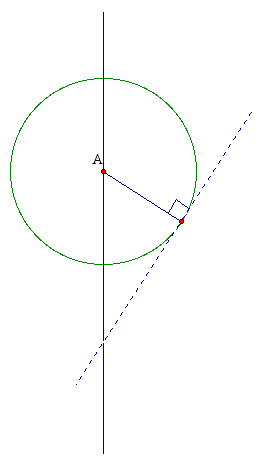
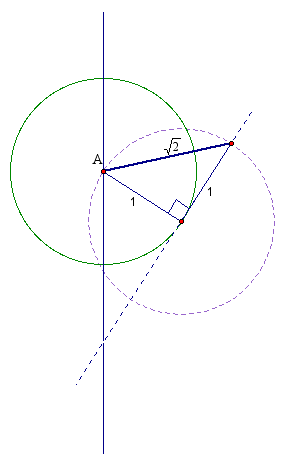
Now we can create our circle with radius to find point I.

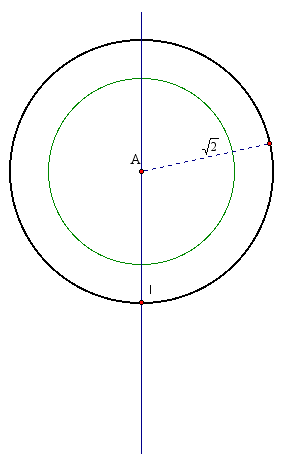
Now wer are left to construct line through I that is perpendicular to the original line and construct the points B and C which are a distance of 0.5 from I and on the new line.

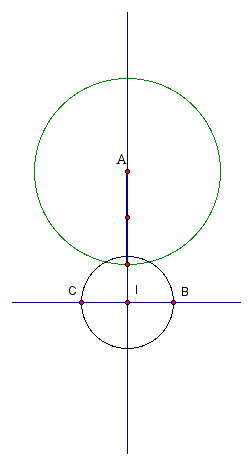
Finally, we construct the circles with center B (or C) that pass through point I,

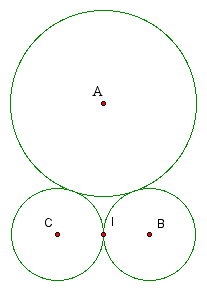
A proof that these are tangent.

This process can be reiterated, with each of the small circles acting as a new large circle. The result is something like this . . .